早教吧作业答案频道 -->数学-->
如图,已知△ABC为等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.(1)写出图中所有的等腰三角形,不需证明;(2)请你判断AD与BE是否垂直,并说明理由;(3)如果BC=12
题目详情
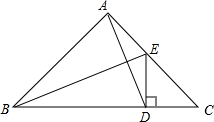
如图,已知△ABC为等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.
(1)写出图中所有的等腰三角形,不需证明;
(2)请你判断AD与BE是否垂直,并说明理由;
(3)如果BC=12,求AB+AE的长.


(1)写出图中所有的等腰三角形,不需证明;
(2)请你判断AD与BE是否垂直,并说明理由;
(3)如果BC=12,求AB+AE的长.

▼优质解答
答案和解析
(1)△ABC、△ABD、△AED、△EDC;
(2)AD⊥BE.
理由:在△ABE和△DBE中,
,
∴△ABE≌△DBE(ASA).
∴AE=DE,AB=BD,
∴B和E在AD的中垂线上.
∴AD⊥BE;
(3)∵△ABC为等腰直角三角形,
∴∠C=45°,
∴直角△EDC是等腰直角三角形,
∴DE=AE.
∴AB+AE=BD+DE=BD+DC=BC=12(cm).
∠BAE=∠BDE BE=BE ∠ABE=∠DBE ∠BAE=∠BDE ∠BAE=∠BDE ∠BAE=∠BDEBE=BE BE=BE BE=BE∠ABE=∠DBE ∠ABE=∠DBE ∠ABE=∠DBE
∴△ABE≌△DBE(ASA).
∴AE=DE,AB=BD,
∴B和E在AD的中垂线上.
∴AD⊥BE;
(3)∵△ABC为等腰直角三角形,
∴∠C=45°,
∴直角△EDC是等腰直角三角形,
∴DE=AE.
∴AB+AE=BD+DE=BD+DC=BC=12(cm).

(2)AD⊥BE.
理由:在△ABE和△DBE中,
|
∴△ABE≌△DBE(ASA).
∴AE=DE,AB=BD,
∴B和E在AD的中垂线上.
∴AD⊥BE;
(3)∵△ABC为等腰直角三角形,
∴∠C=45°,
∴直角△EDC是等腰直角三角形,
∴DE=AE.
∴AB+AE=BD+DE=BD+DC=BC=12(cm).
|
| ∠BAE=∠BDE |
| BE=BE |
| ∠ABE=∠DBE |
| ∠BAE=∠BDE |
| BE=BE |
| ∠ABE=∠DBE |
| ∠BAE=∠BDE |
| BE=BE |
| ∠ABE=∠DBE |
| ∠BAE=∠BDE |
| BE=BE |
| ∠ABE=∠DBE |
∴△ABE≌△DBE(ASA).
∴AE=DE,AB=BD,
∴B和E在AD的中垂线上.
∴AD⊥BE;
(3)∵△ABC为等腰直角三角形,
∴∠C=45°,
∴直角△EDC是等腰直角三角形,
∴DE=AE.
∴AB+AE=BD+DE=BD+DC=BC=12(cm).
看了 如图,已知△ABC为等腰直角...的网友还看了以下:
二进制补码溢出的判断方法,如t=a+b的判断方法(a 2020-04-26 …
以下符合谈判礼仪的是A会面、离别握手时,主人应先向客人先伸手B如果谈判一方的代表同时介绍双方的谈判 2020-05-13 …
英语翻译优势.分析企业在此谈判中所具有的优势,可以使谈判人员发挥这些优势,有利于取得良好的谈判效果 2020-05-17 …
如图是在显微镜下观察到的小鱼尾鳍内血液流动示意图.图中箭头表示血液流动方向,据图回答:图中A是判断 2020-07-01 …
.如果以链表作为栈的存储结构,则退栈操作时()。A.必须判别栈是否满B.判别栈元素的类型c.必须判 2020-07-10 …
求解一道数学题,题目三分钟后打出如果三个非零有理数a、b、c满足关系式a+b+c=0,那么它们的积 2020-07-28 …
题目三分钟后打出如果两个非零有理数a、b满足关系式a+b=0,那么它们的积a×b是正数还是负数,你 2020-07-28 …
用b²-4ac判别一次函数与反比例函数的交点?如题注意:请诸位仔细审题,不要和我说判别式判别二次函 2020-08-01 …
vba里如何判断一个数是不是0.15的倍数假如A1=0.15A2=2.5A3=4.45,我想B列判断 2020-10-31 …
在性质判断的对当关系中,如两个判断是互相矛盾的,那么它们 A.常项和变项都相同B在性质判断的对当关系 2020-11-02 …