早教吧作业答案频道 -->数学-->
设P为曲线C:y=x2+2x+3上的点,且曲线C在点P处切线倾斜角的取值范围为[],则点P横坐标的取值范围为()A.(-∞,]B.[-1,0]C.[0,1]D.[,+∞]
题目详情
设P为曲线C:y=x 2 +2x+3上的点,且曲线C在点P处切线倾斜角的取值范围为[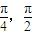 ],则点P横坐标的取值范围为( )
],则点P横坐标的取值范围为( )
A.(-∞, ]
]
B.[-1,0]
C.[0,1]
D.[ ,+∞]
,+∞]
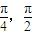 ],则点P横坐标的取值范围为( )
],则点P横坐标的取值范围为( )A.(-∞,
 ]
]B.[-1,0]
C.[0,1]
D.[
 ,+∞]
,+∞] 设P为曲线C:y=x 2 +2x+3上的点,且曲线C在点P处切线倾斜角的取值范围为[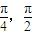 ],则点P横坐标的取值范围为( )
],则点P横坐标的取值范围为( )
A.(-∞, ]
]
B.[-1,0]
C.[0,1]
D.[ ,+∞]
,+∞]
2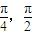 ],则点P横坐标的取值范围为( )
],则点P横坐标的取值范围为( )A.(-∞,
 ]
]B.[-1,0]
C.[0,1]
D.[
 ,+∞]
,+∞]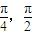


▼优质解答
答案和解析
分析:
根据题意知,倾斜角的取值范围,可以得到曲线C在点P处斜率的取值范围,进而得到点P横坐标的取值范围.
设点P的横坐标为x,∵y=x2+2x+3,∴y'=2x+2,利用导数的几何意义得2x+2=tanα(α为点P处切线的倾斜角),又∵,∴1≤2x+2,∴x∈[,+∞)故选D.
点评:
本小题主要考查利用导数的几何意义求切线斜率问题,解题时要认真审题,仔细解答,属于基础题.
分析:
根据题意知,倾斜角的取值范围,可以得到曲线C在点P处斜率的取值范围,进而得到点P横坐标的取值范围.
设点P的横坐标为x,∵y=x2+2x+3,∴y'=2x+2,利用导数的几何意义得2x+2=tanα(α为点P处切线的倾斜角),又∵,∴1≤2x+2,∴x∈[,+∞)故选D.
点评:
本小题主要考查利用导数的几何意义求切线斜率问题,解题时要认真审题,仔细解答,属于基础题.
分析:
根据题意知,倾斜角的取值范围,可以得到曲线C在点P处斜率的取值范围,进而得到点P横坐标的取值范围.
设点P的横坐标为x,∵y=x2+2x+3,∴y'=2x+2,利用导数的几何意义得2x+2=tanα(α为点P处切线的倾斜角),又∵,∴1≤2x+2,∴x∈[,+∞)故选D.
点评:
本小题主要考查利用导数的几何意义求切线斜率问题,解题时要认真审题,仔细解答,属于基础题.
分析:
根据题意知,倾斜角的取值范围,可以得到曲线C在点P处斜率的取值范围,进而得到点P横坐标的取值范围.
设点P的横坐标为x,∵y=x2+2x+3,∴y'=2x+2,利用导数的几何意义得2x+2=tanα(α为点P处切线的倾斜角),又∵,∴1≤2x+2,∴x∈[,+∞)故选D.
点评:
本小题主要考查利用导数的几何意义求切线斜率问题,解题时要认真审题,仔细解答,属于基础题.
看了 设P为曲线C:y=x2+2x...的网友还看了以下:
有理数的除法法则:(1)两数相除(被除数不为0),同号得,异号得,并把相除;(2)除以一个不为0的 2020-06-27 …
如图,线段A1B1是线段AB平移后得到的.若点C(a,b)是线段AB上的任意一点,当AB平移到A1 2020-07-09 …
2008年8月8日,第29届奥运会在北京隆重开幕,中国约有840000000人观看了开幕式.第29 2020-07-11 …
(2013•山西模拟)在研究小车速度随时间变化关系的实验中,让小车在橡皮筋的作用下从静止弹出,打点 2020-07-14 …
(2008•黄冈模拟)如图,一高为h=0.2m的木板B置于粗糙水平地面上,B的上表面以O点为界,O 2020-07-20 …
如图所示,长为a宽为b的矩形区域内(包括边界)有磁感应强度为B的匀强磁场,磁场方向垂直纸面向外.0 2020-07-22 …
海水受日月的引力而产生潮汐现象,早晨海水上涨叫做潮,黄昏海水上涨叫汐,合称潮汐,潮汐与人类的生活有着 2020-11-04 …
甲、乙、丙三人掷骰子,每人掷三次,他们掷出的点数的积都是24.将每人掷出的点数的和由大到小排列,依次 2020-11-18 …
打点计时器是测量的工具.如图是打出的一条纸带,其相邻两点之间的时间间隔是(选“一定”或“不一定”)相 2020-12-01 …
2008年8月8日,第29届奥运会在北京隆重开幕,中国约有840000000人观看了开幕式.第29届 2020-12-17 …