早教吧作业答案频道 -->数学-->
11、如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式a2-b2=（a+b）（a-b）．
题目详情
11、如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式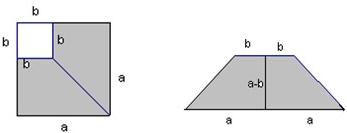
a 2 -b 2 =（a+b）（a-b）
． 11、如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式
a 2 -b 2 =（a+b）（a-b）
． 11、如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式
a 2 -b 2 =（a+b）（a-b）
． a 2 -b 2 =（a+b）（a-b）
2 2▼优质解答
答案和解析
分析：左图中阴影部分的面积是a2-b2，右图中梯形的面积是$frac{1}{2}$（2a+2b）（a-b）=（a+b）（a-b），根据面积相等即可解答．a2-b2=（a+b）（a-b）．点评：此题主要考查的是平方差公式的几何表示，运用不同方法表示阴影部分面积是解题的关键．
分析：左图中阴影部分的面积是a2-b2，右图中梯形的面积是$frac{1}{2}$（2a+2b）（a-b）=（a+b）（a-b），根据面积相等即可解答．a2-b2=（a+b）（a-b）．点评：此题主要考查的是平方差公式的几何表示，运用不同方法表示阴影部分面积是解题的关键．
看了 11、如图，在边长为a的正方...的网友还看了以下：
A和B都是仅由氮和氧两种元素组成的化合物,这两种物质中旦氧元素的质量比都是7:16,但B的相对分子 2020-04-27 …
（1）在四边形ABCD中，∠A的两条边与∠C的两条边互相垂直，且∠A-∠C=60°，则∠A=，∠B 2020-05-01 …
丁基橡胶可用于制造汽车内胎，合成丁基橡胶的一种单体A的分子式为C4H8，A氢化（与H2加成）后得到 2020-05-12 …
这是关于线性代数的问题: 就是在这里说了句因为矩阵A^k,A^l和E都是可交换的,所以矩阵A的两个 2020-05-13 …
已知ab为两个连续的整数,且b比a的两倍小1,则a+b等于多少 2020-05-13 …
已知a的2次方减ab等于21,ab减b的两次方等于负15,求a的2次方减b两次方与a的两次方减2a 2020-05-14 …
（8分）丁基橡胶可用于制造汽车内胎，合成丁基橡胶的一种单体A的分子式为C4H8，A氢化后得到2— 2020-05-14 …
丁基橡胶可用于制造汽车内胎，合成丁基橡胶的一种单体A的分子式为C4H8，A氢化后得到2—甲基丙烷 2020-05-14 …
七年级上学期数学中的（在括号内填上适当的多项式）是什么意思?1.（3乘以a的两次方乘以b-2乘以a 2020-05-20 …
数列{an(n标在右下角)}中a1(1标在右下角)an加1(n加1标在a的右下角)=3an(n标在 2020-06-03 …