早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:3.(1)求∠ADC的度数;(2)利用已知条件和第(1)小题的结论求tan15°的值(结果保留根号).
题目详情
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:
.
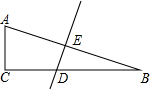
(1)求∠ADC的度数;
(2)利用已知条件和第(1)小题的结论求tan15°的值(结果保留根号).如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:
.

(1)求∠ADC的度数;
(2)利用已知条件和第(1)小题的结论求tan15°的值(结果保留根号).
.

(1)求∠ADC的度数;
(2)利用已知条件和第(1)小题的结论求tan15°的值(结果保留根号).
3 3 3

| 3 |

(1)求∠ADC的度数;
(2)利用已知条件和第(1)小题的结论求tan15°的值(结果保留根号).如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:
| 3 |

(1)求∠ADC的度数;
(2)利用已知条件和第(1)小题的结论求tan15°的值(结果保留根号).
| 3 |

(1)求∠ADC的度数;
(2)利用已知条件和第(1)小题的结论求tan15°的值(结果保留根号).
| 3 |

▼优质解答
答案和解析
(1)连接AD,如图.
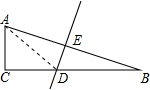 设BD=2k,则CD=
设BD=2k,则CD=
k.
∵DE垂直平分AB,
∴AD=BD=2k.
在Rt△ACD中,
∵∠C=90°,
∴cos∠ADC=
=
=
,
∴∠ADC=30°;
(2)∵AD=BD,
∴∠B=∠DAB.
∵∠ADC=30°,∠B+∠DAB=∠ADC,
∴∠B=∠DAB=15°.
在Rt△ACD中,
∵∠C=90°,
∴AC=
=k.
在Rt△ABC中
∵∠C=90°,
∴tanB=
=
=2-
,
∴tan15°=2-
.
3 3 3 3k.
∵DE垂直平分AB,
∴AD=BD=2k.
在Rt△ACD中,
∵∠C=90°,
∴cos∠ADC=
=
=
,
∴∠ADC=30°;
(2)∵AD=BD,
∴∠B=∠DAB.
∵∠ADC=30°,∠B+∠DAB=∠ADC,
∴∠B=∠DAB=15°.
在Rt△ACD中,
∵∠C=90°,
∴AC=
=k.
在Rt△ABC中
∵∠C=90°,
∴tanB=
=
=2-
,
∴tan15°=2-
.
CD AD CD CD CDAD AD AD=
=
,
∴∠ADC=30°;
(2)∵AD=BD,
∴∠B=∠DAB.
∵∠ADC=30°,∠B+∠DAB=∠ADC,
∴∠B=∠DAB=15°.
在Rt△ACD中,
∵∠C=90°,
∴AC=
=k.
在Rt△ABC中
∵∠C=90°,
∴tanB=
=
=2-
,
∴tan15°=2-
.
k2k
k
k
3 3 3 3k2k 2k 2k=
,
∴∠ADC=30°;
(2)∵AD=BD,
∴∠B=∠DAB.
∵∠ADC=30°,∠B+∠DAB=∠ADC,
∴∠B=∠DAB=15°.
在Rt△ACD中,
∵∠C=90°,
∴AC=
=k.
在Rt△ABC中
∵∠C=90°,
∴tanB=
=
=2-
,
∴tan15°=2-
.
2
3 3 3 32 2 2,
∴∠ADC=30°;
(2)∵AD=BD,
∴∠B=∠DAB.
∵∠ADC=30°,∠B+∠DAB=∠ADC,
∴∠B=∠DAB=15°.
在Rt△ACD中,
∵∠C=90°,
∴AC=
=k.
在Rt△ABC中
∵∠C=90°,
∴tanB=
=
=2-
,
∴tan15°=2-
. AC=
AD2-CD2 AD2-CD2 AD2-CD2 AD2-CD22-CD22=k.
在Rt△ABC中
∵∠C=90°,
∴tanB=
=
=2-
,
∴tan15°=2-
. tanB=
AC BC AC AC ACBC BC BC=
k
k+2kk k k
k+2k
k+2k
3 3 3 3k+2k=2-
3 3 3 3,
∴tan15°=2-
. tan15°=2-
3 3 3 3.
 设BD=2k,则CD=
设BD=2k,则CD=| 3 |
∵DE垂直平分AB,
∴AD=BD=2k.
在Rt△ACD中,
∵∠C=90°,
∴cos∠ADC=
| CD |
| AD |
| ||
| 2k |
| ||
| 2 |
∴∠ADC=30°;
(2)∵AD=BD,
∴∠B=∠DAB.
∵∠ADC=30°,∠B+∠DAB=∠ADC,
∴∠B=∠DAB=15°.
在Rt△ACD中,
∵∠C=90°,
∴AC=
| AD2-CD2 |
在Rt△ABC中
∵∠C=90°,
∴tanB=
| AC |
| BC |
| k | ||
|
| 3 |
∴tan15°=2-
| 3 |
| 3 |
∵DE垂直平分AB,
∴AD=BD=2k.
在Rt△ACD中,
∵∠C=90°,
∴cos∠ADC=
| CD |
| AD |
| ||
| 2k |
| ||
| 2 |
∴∠ADC=30°;
(2)∵AD=BD,
∴∠B=∠DAB.
∵∠ADC=30°,∠B+∠DAB=∠ADC,
∴∠B=∠DAB=15°.
在Rt△ACD中,
∵∠C=90°,
∴AC=
| AD2-CD2 |
在Rt△ABC中
∵∠C=90°,
∴tanB=
| AC |
| BC |
| k | ||
|
| 3 |
∴tan15°=2-
| 3 |
| CD |
| AD |
| ||
| 2k |
| ||
| 2 |
∴∠ADC=30°;
(2)∵AD=BD,
∴∠B=∠DAB.
∵∠ADC=30°,∠B+∠DAB=∠ADC,
∴∠B=∠DAB=15°.
在Rt△ACD中,
∵∠C=90°,
∴AC=
| AD2-CD2 |
在Rt△ABC中
∵∠C=90°,
∴tanB=
| AC |
| BC |
| k | ||
|
| 3 |
∴tan15°=2-
| 3 |
| ||
| 2k |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
∴∠ADC=30°;
(2)∵AD=BD,
∴∠B=∠DAB.
∵∠ADC=30°,∠B+∠DAB=∠ADC,
∴∠B=∠DAB=15°.
在Rt△ACD中,
∵∠C=90°,
∴AC=
| AD2-CD2 |
在Rt△ABC中
∵∠C=90°,
∴tanB=
| AC |
| BC |
| k | ||
|
| 3 |
∴tan15°=2-
| 3 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
∴∠ADC=30°;
(2)∵AD=BD,
∴∠B=∠DAB.
∵∠ADC=30°,∠B+∠DAB=∠ADC,
∴∠B=∠DAB=15°.
在Rt△ACD中,
∵∠C=90°,
∴AC=
| AD2-CD2 |
在Rt△ABC中
∵∠C=90°,
∴tanB=
| AC |
| BC |
| k | ||
|
| 3 |
∴tan15°=2-
| 3 |
| AD2-CD2 |
在Rt△ABC中
∵∠C=90°,
∴tanB=
| AC |
| BC |
| k | ||
|
| 3 |
∴tan15°=2-
| 3 |
| AC |
| BC |
| k | ||
|
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
∴tan15°=2-
| 3 |
| 3 |
看了 如图,在Rt△ABC中,∠C...的网友还看了以下:
音标左下角的小逗号是什么意思?我是初中生,每次查字典看音标的时候,知道右上角的音标是着重的意思,那 2020-05-20 …
改错.四个括号中哪个错了,改到后面的小括号1Mikefavoritesubjectisscienc 2020-06-02 …
负荆请罪剧中的方括号内主要什么交代和什么剧中的小括号内交代什么等. 2020-06-15 …
关于小括号与中括号的问题中括号里的小括号去掉之后,中括号需要变成小括号,还是不变,直接抄下中括号呢 2020-06-24 …
小括号x方减x括起来的平方减五倍的小括号x方减x括起来加六等于�� 2020-07-11 …
如何使用word2000以上版本输入英语音标中的连读符号在使用word输入英语音标时经常需要输入连 2020-07-21 …
c#怎么能让文本框中只能输入正负数字(包括小数),加减乘除号,还有英文下的小括号?能都写在ONKE 2020-07-23 …
VB里面WHILE(INP(642)AND12)12:里面的小于号和大于号什么意思?RT 2020-08-01 …
等号上面加一个顺时针旋转90度的小于号表示什么? 2020-08-01 …
音标左下角的小逗号是什么意思?我是初中生,每次查字典看音标的时候,知道右上角的音标是着重的意思,那左 2020-12-02 …