早教吧作业答案频道 -->数学-->
操作与探究在Rt△ABC中,∠C=90°,AB=5,AC=3,点O是AB的中点,将一块直角三角板ODE的直角顶点绕点0旋转,边OD、OE分别与△ABC的边BC、AC交于点N、M(1)如图一,当三角板的一条直角边与AB重合
题目详情
操作与探究
在Rt△ABC中,∠C=90°,AB=5,AC=3,点O是AB的中点,将一块直角三角板ODE的直角顶点绕点0旋转,边OD、OE分别与△ABC的边BC、AC交于点N、M
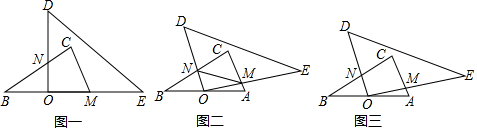
(1)如图一,当三角板的一条直角边与AB重合时,点M与点A也重合,求此时CN的长;写出AC2、CN2、BN2满足的数量关系:
(2)当三角板旋转到如图二所示的位置时,即点M在AC上(不与A、C重合),猜想图二中AM2、BN2、MN2满足的数量关系:说明你得出此结论的理由.
(3)若在三角板旋转的过程中满足CM=CN,请你利用图三,求出此时BN的长.
 操作与探究
操作与探究
在Rt△ABC中,∠C=90°,AB=5,AC=3,点O是AB的中点,将一块直角三角板ODE的直角顶点绕点0旋转,边OD、OE分别与△ABC的边BC、AC交于点N、M
(1)如图一,当三角板的一条直角边与AB重合时,点M与点A也重合,求此时CN的长;写出AC2、CN2、BN2满足的数量关系:
(2)当三角板旋转到如图二所示的位置时,即点M在AC上(不与A、C重合),猜想图二中AM2、BN2、MN2满足的数量关系:说明你得出此结论的理由.
(3)若在三角板旋转的过程中满足CM=CN,请你利用图三,求出此时BN的长.

222
222

在Rt△ABC中,∠C=90°,AB=5,AC=3,点O是AB的中点,将一块直角三角板ODE的直角顶点绕点0旋转,边OD、OE分别与△ABC的边BC、AC交于点N、M
(1)如图一,当三角板的一条直角边与AB重合时,点M与点A也重合,求此时CN的长;写出AC2、CN2、BN2满足的数量关系:
(2)当三角板旋转到如图二所示的位置时,即点M在AC上(不与A、C重合),猜想图二中AM2、BN2、MN2满足的数量关系:说明你得出此结论的理由.
(3)若在三角板旋转的过程中满足CM=CN,请你利用图三,求出此时BN的长.
 操作与探究
操作与探究在Rt△ABC中,∠C=90°,AB=5,AC=3,点O是AB的中点,将一块直角三角板ODE的直角顶点绕点0旋转,边OD、OE分别与△ABC的边BC、AC交于点N、M
(1)如图一,当三角板的一条直角边与AB重合时,点M与点A也重合,求此时CN的长;写出AC2、CN2、BN2满足的数量关系:
(2)当三角板旋转到如图二所示的位置时,即点M在AC上(不与A、C重合),猜想图二中AM2、BN2、MN2满足的数量关系:说明你得出此结论的理由.
(3)若在三角板旋转的过程中满足CM=CN,请你利用图三,求出此时BN的长.

222
222

▼优质解答
答案和解析
(1)在Rt△ABC中,∠C=90°,AB=5,AC=3,∴BC=4,∵点O是AB的中点,∴OB=12BM=12AB=52,当三角板的一条直角边与AB重合时,点M与点A也重合,∴BM=AB=5,∠BON=90°,∵∠C=90°,∴∠BON=∠C=90°,∵∠B=∠B,∴△...
看了 操作与探究在Rt△ABC中,...的网友还看了以下:
数学题: 已知抛物线y=x²+bx+c交x轴于A(1,0),B(3,0), 交y轴于点C,其顶点为 2020-05-13 …
二次函数y=ax^2+bx+c(a不等于0)图像的顶点为D,其图像与x轴的交点A、B的横坐标是-1 2020-05-16 …
如图,二次函数y=ax^2+bx+c的图像交x轴于A(-2,0)B(1,0)交y轴于点C(0,-2 2020-05-16 …
1)已知f(x)=ax的平方+bx+c满足f(1)=0,a>b>c①求c/a的取值范围②若该函数图 2020-05-20 …
已知函数f(x)=ax^2+2bx+c(a不等于0),a,b,c为实数,且a>b>c,a+b+c= 2020-06-12 …
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在 2020-07-09 …
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在 2020-07-31 …
如图,抛物线y=ax2+bx+c经过点(-1,0),与x轴的另一个交点在点(2,0)和点(3,0)之 2020-11-01 …
如图所示,抛物线y=ax2+bx+c的顶点为B(-1,3),与x轴的交点A在点(-3,0)和(-2, 2020-11-01 …
在直角坐标系中,抛物线y=ax平方+bx+c(a不等于0)与x轴交点A(-1,0)、B(3,0)交y 2021-01-10 …