早教吧作业答案频道 -->数学-->
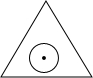
如图,一个半径为r的圆形纸片在边长为a(a≥23r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是.
题目详情
如图,一个半径为r的圆形纸片在边长为a(a≥2
r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是___.
r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是___.

3 3 3

| | 3 |

| | 3 |

| | 3 |

▼优质解答
答案和解析
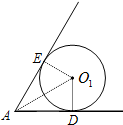 如图,当圆形纸片运动到与∠A的两边相切的位置时,
如图,当圆形纸片运动到与∠A的两边相切的位置时,
过圆形纸片的圆心O11作两边的垂线,垂足分别为D,E,
连结AO11,则Rt△ADO11中,∠O11AD=30°,O11D=r,AD=
r,
∴S△ADO1=
O1D•AD=
r2.由S四边形ADO1E=2S△ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2.
3 3 3 3r,
∴S△ADO1=
O1D•AD=
r2.由S四边形ADO1E=2S△ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. S△ADO1=
O1D•AD=
r2.由S四边形ADO1E=2S△ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. △ADO1=
O1D•AD=
r2.由S四边形ADO1E=2S△ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. 1=
1 2 1 1 12 2 2O1D•AD=
r2.由S四边形ADO1E=2S△ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. 1D•AD=
2
3 3 3 32 2 2r2.由S四边形ADO1E=2S△ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. 2.由S四边形ADO1E=2S△ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. S四边形ADO1E=2S△ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. 四边形ADO1E=2S△ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. 1E=2S△ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. △ADO1=
r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. 1=
3 3 3 3r2.
∵由题意,∠DO1E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. 2.
∵由题意,∠DO11E=120°,得S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. S扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. 扇形O1DE=
r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. 1DE=
π 3 π π π3 3 3r2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. 2,
∴圆形纸片不能接触到的部分的面积为3(
r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2.
3 3 3 3r2-
r2)=(3
-π)r2.
故答案为:(3
-π)r2. 2-
π 3 π π π3 3 3r2)=(3
-π)r2.
故答案为:(3
-π)r2. 2)=(3
-π)r2.
故答案为:(3
-π)r2.
3 3 3 3-π)r22.
故答案为:(3
-π)r2. (3
3 3 3 3-π)r2. 2.
 如图,当圆形纸片运动到与∠A的两边相切的位置时,
如图,当圆形纸片运动到与∠A的两边相切的位置时,过圆形纸片的圆心O11作两边的垂线,垂足分别为D,E,
连结AO11,则Rt△ADO11中,∠O11AD=30°,O11D=r,AD=
| 3 |
∴S△ADO1=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 3 |
∴S△ADO1=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 3 |
∵由题意,∠DO1E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
∵由题意,∠DO11E=120°,得S扇形O1DE=
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| π |
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
∴圆形纸片不能接触到的部分的面积为3(
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| π |
| 3 |
| 3 |
故答案为:(3
| 3 |
| 3 |
故答案为:(3
| 3 |
| 3 |
故答案为:(3
| 3 |
| 3 |
看了 如图,一个半径为r的圆形纸片...的网友还看了以下:
已知x,y为有理数,如果规定一种运算*,其意义是x*y=xy+1,试根据这种运算完成下列各题.求2 2020-04-09 …
工地上有一堆泥沙,共三吨,刘师傅5小时运完.共3吨,刘师傅5小时运完.他平均每小时运这堆泥沙的几分 2020-04-27 …
工地上有一堆沙,共有3吨,刘师傅5小时运往运完.他平均每小时运这堆沙的几分之几,3小时运这堆沙的几 2020-04-27 …
学校的运动场是有一个长方形和两个半圆组成,共设有6条跑道,每条跑道宽1.2米.1.这个运动场的占地 2020-05-13 …
学校的运动场如图所示,两端为半圆形,中间为长方形,绕场跑3圈共跑了多少米?这个运动场的占地面积是多 2020-05-22 …
一个运动场,两端是半圆形,中间是长方形.围着运动场跑3圈,至少跑了多少米?这个运动场面积是多少?长 2020-05-22 …
一堆煤,第一天运走的吨数与总吨数的比是1:4,第二天运走405吨后,两天正好运走了总数的1/3.这 2020-06-06 …
len(space(3)-space(2))len(space(2)-space(3))这俩运行结 2020-06-15 …
用3辆同样的卡车运162吨苹果,每辆卡车每次运6吨,需要多少次才能把这些苹果全部运完?(1)162 2020-07-18 …
某加工厂将一张矩形的铁皮在四角各剪去一个边长为1m的小正方形后围成一个容积为15m^3的无盖长方体状 2020-12-21 …