如图1和图2，在△ABC中，AB=13，BC=14，cos∠ABC=513．探究：如图1，AH⊥BC于点H，则AH=，AC=，△ABC的面积S△ABC=．拓展：如图2，点D在AC上（可与点A、C重合），分别过点A

Question

如图1和图2，在△ABC中，AB=13，BC=14，cos∠ABC= (5)/(13)．
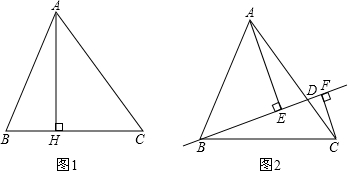
探究：如图1，AH⊥BC于点H，则AH=___，AC=___，△ABC的面积S_△ABC=___．
拓展：如图2，点D在AC上（可与点A、C重合），分别过点A、C作直线BD的垂线，垂足为E、F，设BD=x，AE=m，CF=n，（当点 D与A重合时，我们认为S_△ABD=0）．
（1）用含x、m或n的代数式表示S_△ABD及S_△CBD；
（2）求（m+n）与x的函数关系式，并求（m+n）的最大值和最小值；
（3）对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围．
发现：请你确定一条直线，使得A、B、C三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值．
如图1和图2，在△ABC中，AB=13，BC=14，cos∠ABC= (5)/(13)．
探究：如图1，AH⊥BC于点H，则AH=___，AC=___，△ABC的面积S_△ABC=___．
拓展：如图2，点D在AC上（可与点A、C重合），分别过点A、C作直线BD的垂线，垂足为E、F，设BD=x，AE=m，CF=n，（当点 D与A重合时，我们认为S_△ABD=0）．
（1）用含x、m或n的代数式表示S_△ABD及S_△CBD；
（2）求（m+n）与x的函数关系式，并求（m+n）的最大值和最小值；
（3）对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围．
发现：请你确定一条直线，使得A、B、C三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值．
(5)/(13)．
探究：如图1，AH⊥BC于点H，则AH=___，AC=___，△ABC的面积S_△ABC=___．
拓展：如图2，点D在AC上（可与点A、C重合），分别过点A、C作直线BD的垂线，垂足为E、F，设BD=x，AE=m，CF=n，（当点 D与A重合时，我们认为S_△ABD=0）．
（1）用含x、m或n的代数式表示S_△ABD及S_△CBD；
（2）求（m+n）与x的函数关系式，并求（m+n）的最大值和最小值；
（3）对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围．
发现：请你确定一条直线，使得A、B、C三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值．
(5)/(13) 5 13 5 5 13 13
_{△ABC
△ABD
△ABD△CBD}

Answer 1

探究： ∵在△ABC中，AB=13，BC=14，cos∠ABC=513，∴BHAB=513，∴BH=5，∴AH=132-52=12，∴HC=9，AC=122+92=15，∴△ABC的面积S△ABC=12×12×14=84；故答案为：12，15，84；拓展： （1）由三角形面积公式得出：S△...