某研究所正在研究一种电磁刹车装置，试验小车质量m=2kg，底部有一个匝数n=100匝，边长a=0.01m的线圈，线圈总电阻r=1Ω，在试验中，小车（形状可视为简化为正方形线圈）从轨道起点由静止出

Question

某研究所正在研究一种电磁刹车装置，试验小车质量m=2kg，底部有一个匝数n=100匝，边长a=0.01m的线圈，线圈总电阻r=1Ω，在试验中，小车（形状可视为简化为正方形线圈）从轨道起点由静止出发，通入右边的匀强磁场区域ABCD，BC长d=0.20m，磁感应强度B=1T，磁场方向竖直向上，整个运动过程中不计小车所受的摩擦及空气阻力，小车在轨道连接处运动时无能量损失．

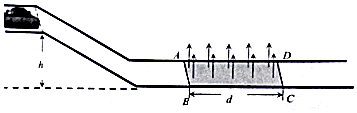
（1）当试验小车从h=1.25m高度无初速度释放，求小车前端刚进入AB边界时产生感应电动势的大小．
（2）在第（1）问，小车进入磁场后作减速运动，当小车末端到达AB边界时速度刚好减为零，求此过程中线圈产生的热量．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，求此高度h′．

Answer 1

（1）小车在斜轨上下滑的过程，根据机械能守恒定律得：
mgh=(1)/(2)mv2
得：v=√(2gh)=√(2×10×1.25)=5m/s
根据法拉第电磁感应定律得小车前端刚进入AB边界时产生感应电动势的大小为：
E=nBav=100×1×0.01×5V=5V
（2）小车进入磁场后作减速运动，动能转化为内能，根据能量守恒定律得此过程中线圈产生的热量为：
Q=(1)/(2)mv2=(1)/(2)×2×5²=25J
（3）设小车前端刚进入AB边界时的速度为v₁，对于线圈进出磁场过程，取向右为正方向，由动量定理得：
-nB

.

I

at=-mv₁，
又通过线圈截面的电荷量为：q=

.

I

t
联立得：q=(mv1)/(nBa)
根据q=n(△Φ)/(R)得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (1)/(2)12111222mv2
得：v=√(2gh)=√(2×10×1.25)=5m/s
根据法拉第电磁感应定律得小车前端刚进入AB边界时产生感应电动势的大小为：
E=nBav=100×1×0.01×5V=5V
（2）小车进入磁场后作减速运动，动能转化为内能，根据能量守恒定律得此过程中线圈产生的热量为：
Q=(1)/(2)mv2=(1)/(2)×2×5²=25J
（3）设小车前端刚进入AB边界时的速度为v₁，对于线圈进出磁场过程，取向右为正方向，由动量定理得：
-nB

.

I

at=-mv₁，
又通过线圈截面的电荷量为：q=

.

I

t
联立得：q=(mv1)/(nBa)
根据q=n(△Φ)/(R)得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． 2
得：v=√(2gh)=√(2×10×1.25)=5m/s
根据法拉第电磁感应定律得小车前端刚进入AB边界时产生感应电动势的大小为：
E=nBav=100×1×0.01×5V=5V
（2）小车进入磁场后作减速运动，动能转化为内能，根据能量守恒定律得此过程中线圈产生的热量为：
Q=(1)/(2)mv2=(1)/(2)×2×5²=25J
（3）设小车前端刚进入AB边界时的速度为v₁，对于线圈进出磁场过程，取向右为正方向，由动量定理得：
-nB

.

I

at=-mv₁，
又通过线圈截面的电荷量为：q=

.

I

t
联立得：q=(mv1)/(nBa)
根据q=n(△Φ)/(R)得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． √(2gh)

2gh

2gh

2gh2gh=√(2×10×1.25)=5m/s
根据法拉第电磁感应定律得小车前端刚进入AB边界时产生感应电动势的大小为：
E=nBav=100×1×0.01×5V=5V
（2）小车进入磁场后作减速运动，动能转化为内能，根据能量守恒定律得此过程中线圈产生的热量为：
Q=(1)/(2)mv2=(1)/(2)×2×5²=25J
（3）设小车前端刚进入AB边界时的速度为v₁，对于线圈进出磁场过程，取向右为正方向，由动量定理得：
-nB

.

I

at=-mv₁，
又通过线圈截面的电荷量为：q=

.

I

t
联立得：q=(mv1)/(nBa)
根据q=n(△Φ)/(R)得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． √(2×10×1.25)

2×10×1.25

2×10×1.25

2×10×1.252×10×1.25=5m/s
根据法拉第电磁感应定律得小车前端刚进入AB边界时产生感应电动势的大小为：
E=nBav=100×1×0.01×5V=5V
（2）小车进入磁场后作减速运动，动能转化为内能，根据能量守恒定律得此过程中线圈产生的热量为：
Q=(1)/(2)mv2=(1)/(2)×2×5²=25J
（3）设小车前端刚进入AB边界时的速度为v₁，对于线圈进出磁场过程，取向右为正方向，由动量定理得：
-nB

.

I

at=-mv₁，
又通过线圈截面的电荷量为：q=

.

I

t
联立得：q=(mv1)/(nBa)
根据q=n(△Φ)/(R)得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (1)/(2)12111222mv2=(1)/(2)×2×5²=25J
（3）设小车前端刚进入AB边界时的速度为v₁，对于线圈进出磁场过程，取向右为正方向，由动量定理得：
-nB

.

I

at=-mv₁，
又通过线圈截面的电荷量为：q=

.

I

t
联立得：q=(mv1)/(nBa)
根据q=n(△Φ)/(R)得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． 2=(1)/(2)×2×5²=25J
（3）设小车前端刚进入AB边界时的速度为v₁，对于线圈进出磁场过程，取向右为正方向，由动量定理得：
-nB

.

I

at=-mv₁，
又通过线圈截面的电荷量为：q=

.

I

t
联立得：q=(mv1)/(nBa)
根据q=n(△Φ)/(R)得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (1)/(2)12111222×2×5²2=25J
（3）设小车前端刚进入AB边界时的速度为v₁1，对于线圈进出磁场过程，取向右为正方向，由动量定理得：
-nB

.

I

at=-mv₁，
又通过线圈截面的电荷量为：q=

.

I

t
联立得：q=(mv1)/(nBa)
根据q=n(△Φ)/(R)得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m．

.

I

.

I

.

.

.

.IIIat=-mv₁1，
又通过线圈截面的电荷量为：q=

.

I

t
联立得：q=(mv1)/(nBa)
根据q=n(△Φ)/(R)得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m．

.

I

.

I

.

.

.

.IIIt
联立得：q=(mv1)/(nBa)
根据q=n(△Φ)/(R)得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (mv1)/(nBa)mv1nBamv1mv1mv11nBanBanBa
根据q=n(△Φ)/(R)得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (△Φ)/(R)△ΦR△Φ△Φ△ΦRRR得线圈进入磁场的过程，通过线圈截面的电荷量为：
q₁1=n(Ba2)/(r)=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (Ba2)/(r)Ba2rBa2Ba2Ba22rrr=100×(1×0.012)/(1)=0.01C
则有：q=2q₁=0.02C
所以有：v₁=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (1×0.012)/(1)1×0.01211×0.0121×0.0121×0.0122111=0.01C
则有：q=2q₁1=0.02C
所以有：v₁1=(nqBa)/(m)=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (nqBa)/(m)nqBamnqBanqBanqBammm=(100×0.02×1×0.01)/(2)=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (100×0.02×1×0.01)/(2)100×0.02×1×0.012100×0.02×1×0.01100×0.02×1×0.01100×0.02×1×0.01222=0.01m/s
依据机械能守恒定律，则有：mgh′=(1)/(2)m

v

2 1

代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (1)/(2)12111222m

v

2 1

v

2

1

v

2

1

vv

2

1

2

2

1

1
代入数据，解得：h′=(v21)/(2g)=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (v21)/(2g)

v

2 1

2g

v

2 1

v

2 1

v

2 1

v

2

1

v

2

1

vv

2

1

2

2

1

12g2g2g=(0.012)/(2×10)=5×10^-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6m． (0.012)/(2×10)0.0122×100.0120.0120.01222×102×102×10=5×10^-6-6m
答：（1）小车前端刚进入AB边界时产生感应电动势的大小5V．
（2）当小车末端到达AB边界时速度刚好减为零，此过程中线圈产生的热量25J．
（3）再次改变小车释放的高度，使得小车尾端刚好能到达CD处，此高度5×10^-6-6m．