早教吧作业答案频道 -->数学-->
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴
题目详情
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长___.
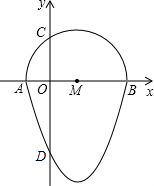 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长___.
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长___.
 2
2

 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长___.
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2-2x-3,求这个“果圆”被y轴截得线段CD的长___. 2
2
▼优质解答
答案和解析
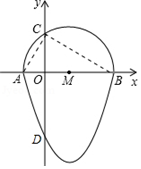 连接AC,BC.
连接AC,BC.
∵抛物线的解析式为y=x22-2x-3,
∴点D的坐标为(0,-3),
∴OD的长为3.
设y=0,则0=x22-2x-3,解得:x=-1或3,
∴A(-1,0),B(3,0).
∴AO=1,BO=3,AB=4,M(1,0).
∴MC=2,OM=1.
在Rt△COB中,OC=
=
.
∴CD=CO+OD=3+
,即这个“果圆”被y轴截得的线段CD的长3+
.
故答案为:3+
.
CM2-OM2 CM2-OM2 CM2-OM2 CM2-OM22-OM22=
.
∴CD=CO+OD=3+
,即这个“果圆”被y轴截得的线段CD的长3+
.
故答案为:3+
.
3 3 3 3.
∴CD=CO+OD=3+
,即这个“果圆”被y轴截得的线段CD的长3+
.
故答案为:3+
.
3 3 3 3,即这个“果圆”被y轴截得的线段CD的长3+
.
故答案为:3+
.
3 3 3 3.
故答案为:3+
.
3 3 3 3.
 连接AC,BC.
连接AC,BC.∵抛物线的解析式为y=x22-2x-3,
∴点D的坐标为(0,-3),
∴OD的长为3.
设y=0,则0=x22-2x-3,解得:x=-1或3,
∴A(-1,0),B(3,0).
∴AO=1,BO=3,AB=4,M(1,0).
∴MC=2,OM=1.
在Rt△COB中,OC=
| CM2-OM2 |
| 3 |
∴CD=CO+OD=3+
| 3 |
| 3 |
故答案为:3+
| 3 |
| CM2-OM2 |
| 3 |
∴CD=CO+OD=3+
| 3 |
| 3 |
故答案为:3+
| 3 |
| 3 |
∴CD=CO+OD=3+
| 3 |
| 3 |
故答案为:3+
| 3 |
| 3 |
| 3 |
故答案为:3+
| 3 |
| 3 |
故答案为:3+
| 3 |
| 3 |
看了 如图,我们把一个半圆与抛物线...的网友还看了以下:
西班牙语语法buendía和buenosdías有什么区别buendía和buenosdías有什 2020-04-27 …
有没有人知道考三副甲乙丙的英语有什么区别我知道甲类和丙类的大体区别了那乙类是什么难度呢?是在甲丙之 2020-05-15 …
已知平面π:2x+y+z=3和直线L:x+2y+z=1;x+y+2z=4.求直线L的对称式方程,平 2020-05-16 …
愠怒和愤怒的区别我知道这两个词意思都差不多,不过肯定有一些差别的,不然为什么会有这“两个”词而不是 2020-05-16 …
关于BUSINESSSTATISTICS的问题在QUANTITATIVEDATA里面分成RATIO 2020-05-17 …
普通话发音:津和京的区别我知道它们一个是前鼻音一个是后鼻音,但我读起来别人听着都一样.可不可以教我 2020-05-23 …
异面直线与共面怎么区别我知道:不同在任何一个平面内的两条直线叫做异面直线.既不平行,也不相交.可我 2020-07-13 …
载货清单和装箱清单的区别我知道载货清单manifest:亦称舱单.船方或其代理人对全船所载货物编造的 2020-11-28 …
learned和learnt的区别作为过去式和过去分词使用的时候的区别,不是指learned做形容词 2020-12-02 …
匀变速直线运动平均速度公式使用的区别我知道有V平均=(V初+V末)/2和V平均=△x/t,想知道这两 2020-12-09 …