早教吧 育儿知识 作业答案 考试题库 百科 知识分享
早教吧作业答案频道 -->数学-->

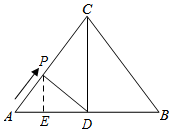
如图，△ABC中，AC=BC=10cm，AB=12cm，点D是AB的中点，连结CD，动点P从点A出发，沿A→C→B的路径运动，到达点B时运动停止，速度为每秒2cm，设运动时间为t秒．（1）求CD的长；（2）当t为何值时

题目详情
如图，△ABC中，AC=BC=10cm，AB=12cm，点D是AB的中点，连结CD，动点P从点A出发，沿A→C→B的路径运动，到达点B时运动停止，速度为每秒2cm，设运动时间为t秒．
作业帮
（1）求CD的长；
（2）当t为何值时，△ADP是直角三角形？
（3）直接写出：当t为何值时，△ADP是等腰三角形？如图，△ABC中，AC=BC=10cm，AB=12cm，点D是AB的中点，连结CD，动点P从点A出发，沿A→C→B的路径运动，到达点B时运动停止，速度为每秒2cm，设运动时间为t秒．
作业帮
（1）求CD的长；
（2）当t为何值时，△ADP是直角三角形？
（3）直接写出：当t为何值时，△ADP是等腰三角形？
作业帮


▼优质解答
答案和解析
（1）如图所示，AC=BC=10cm，AB=12cm，点D是AB的中点，
作业帮
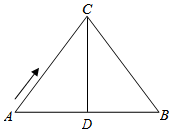
∴CD⊥AB，AD=DB=
1
2
AB=6cm，
∴Rt△ACD中，CD=
AC2-AD2
=8cm；

（2）分两种情况：
①如图所示，当DP⊥AC时，△ADP是直角三角形，
作业帮
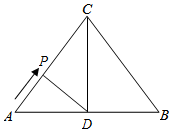
∵∠A=∠A，∠APD=∠ADC=90°，
∴△APD∽△ADC，
∴
AP
AD
=
AD
AC
，即
2t
6
=
6
10
，
解得t=1.8，
②如图所示，当PD⊥AD时，△ADP是直角三角形，
作业帮
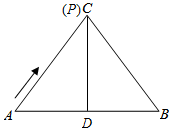
此时点P与点C重合，AP=AC=10，
∴t=
10
2
=5，
综上所述，当t=1.8或5秒时，△ADP是直角三角形；

（3）分三种情况：
①如图所示，当PA=PD时，过点P作PE⊥AD于E，则AE=
1
2
AD=3，
作业帮
∵PE∥CD，
∴△APE∽△ACD，
∴
AP
AC
=
AE
AD
，即
2t
10
=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
1
2
12111222AB=6cm，
∴Rt△ACD中，CD=
AC2-AD2
=8cm；

（2）分两种情况：
①如图所示，当DP⊥AC时，△ADP是直角三角形，
作业帮
∵∠A=∠A，∠APD=∠ADC=90°，
∴△APD∽△ADC，
∴
AP
AD
=
AD
AC
，即
2t
6
=
6
10
，
解得t=1.8，
②如图所示，当PD⊥AD时，△ADP是直角三角形，
作业帮
此时点P与点C重合，AP=AC=10，
∴t=
10
2
=5，
综上所述，当t=1.8或5秒时，△ADP是直角三角形；

（3）分三种情况：
①如图所示，当PA=PD时，过点P作PE⊥AD于E，则AE=
1
2
AD=3，
作业帮
∵PE∥CD，
∴△APE∽△ACD，
∴
AP
AC
=
AE
AD
，即
2t
10
=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
AC2-AD2
AC2-AD2
AC2-AD2
AC2-AD2AC2-AD22-AD22=8cm；

（2）分两种情况：
①如图所示，当DP⊥AC时，△ADP是直角三角形，
作业帮
∵∠A=∠A，∠APD=∠ADC=90°，
∴△APD∽△ADC，
∴
AP
AD
=
AD
AC
，即
2t
6
=
6
10
，
解得t=1.8，
②如图所示，当PD⊥AD时，△ADP是直角三角形，
作业帮
此时点P与点C重合，AP=AC=10，
∴t=
10
2
=5，
综上所述，当t=1.8或5秒时，△ADP是直角三角形；

（3）分三种情况：
①如图所示，当PA=PD时，过点P作PE⊥AD于E，则AE=
1
2
AD=3，
作业帮
∵PE∥CD，
∴△APE∽△ACD，
∴
AP
AC
=
AE
AD
，即
2t
10
=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
AP
AD
APADAPAPAPADADAD=
AD
AC
，即
2t
6
=
6
10
，
解得t=1.8，
②如图所示，当PD⊥AD时，△ADP是直角三角形，
作业帮
此时点P与点C重合，AP=AC=10，
∴t=
10
2
=5，
综上所述，当t=1.8或5秒时，△ADP是直角三角形；

（3）分三种情况：
①如图所示，当PA=PD时，过点P作PE⊥AD于E，则AE=
1
2
AD=3，
作业帮
∵PE∥CD，
∴△APE∽△ACD，
∴
AP
AC
=
AE
AD
，即
2t
10
=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
AD
AC
ADACADADADACACAC，即
2t
6
=
6
10
，
解得t=1.8，
②如图所示，当PD⊥AD时，△ADP是直角三角形，
作业帮
此时点P与点C重合，AP=AC=10，
∴t=
10
2
=5，
综上所述，当t=1.8或5秒时，△ADP是直角三角形；

（3）分三种情况：
①如图所示，当PA=PD时，过点P作PE⊥AD于E，则AE=
1
2
AD=3，
作业帮
∵PE∥CD，
∴△APE∽△ACD，
∴
AP
AC
=
AE
AD
，即
2t
10
=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
2t
6
2t62t2t2t666=
6
10
，
解得t=1.8，
②如图所示，当PD⊥AD时，△ADP是直角三角形，
作业帮
此时点P与点C重合，AP=AC=10，
∴t=
10
2
=5，
综上所述，当t=1.8或5秒时，△ADP是直角三角形；

（3）分三种情况：
①如图所示，当PA=PD时，过点P作PE⊥AD于E，则AE=
1
2
AD=3，
作业帮
∵PE∥CD，
∴△APE∽△ACD，
∴
AP
AC
=
AE
AD
，即
2t
10
=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
6
10
610666101010，
解得t=1.8，
②如图所示，当PD⊥AD时，△ADP是直角三角形，
作业帮
此时点P与点C重合，AP=AC=10，
∴t=
10
2
=5，
综上所述，当t=1.8或5秒时，△ADP是直角三角形；

（3）分三种情况：
①如图所示，当PA=PD时，过点P作PE⊥AD于E，则AE=
1
2
AD=3，
作业帮
∵PE∥CD，
∴△APE∽△ACD，
∴
AP
AC
=
AE
AD
，即
2t
10
=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
10
2
102101010222=5，
综上所述，当t=1.8或5秒时，△ADP是直角三角形；

（3）分三种情况：
①如图所示，当PA=PD时，过点P作PE⊥AD于E，则AE=
1
2
AD=3，
作业帮
∵PE∥CD，
∴△APE∽△ACD，
∴
AP
AC
=
AE
AD
，即
2t
10
=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
1
2
12111222AD=3，
作业帮
∵PE∥CD，
∴△APE∽△ACD，
∴
AP
AC
=
AE
AD
，即
2t
10
=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
AP
AC
APACAPAPAPACACAC=
AE
AD
，即
2t
10
=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
AE
AD
AEADAEAEAEADADAD，即
2t
10
=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
2t
10
2t102t2t2t101010=
3
6
，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
3
6
36333666，
解得t=
5
2
；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
5
2
52555222；
②如图所示，当AP=AD时，2t=6，
作业帮
∴t=
6
2
=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
6
2
62666222=3；
③如图所示，当AD=PD时，过点D作DF⊥AP于F，则AF=
1
2
AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
1
2
12111222AP=t，
作业帮
∵∠A=∠A，∠AFD=∠ADC=90°，
∴△AFD∽△ADC，
∴
AF
AD
=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
AF
AD
AFADAFAFAFADADAD=
AD
AC
，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
AD
AC
ADACADADADACACAC，即
t
6
=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
t
6
t6ttt666=
6
10
，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
6
10
610666101010，
解得t=3.6，
综上所述，当t=2.5或3或3.6秒时，△ADP是等腰三角形．
看了 如图，△ABC中，AC=BC...的网友还看了以下：

如果大气中没有”温室气体”,地球表面温度将降低至-23`C,但是,如果温室气体量增加过多过快，会造 　2020-05-13 …

如果f(t)=t/(1+t),g(t)=t/(1-t),证明：证明：f(t)-g(t)=-2g（t 　2020-05-23 …

食品单位C/t是什么意思 　2020-06-08 …

方程中a.x.c.t是表示什么呀~就是a.x.c.t表示的数字是什么,也就是a等于几,x等于几,c 　2020-06-12 …

关于arctan积分的问题我们都知道∫1/(x^2+1)dx=arctanx+C但是如果分解x^2 　2020-06-13 …

会追加急二次函数解析式如何带入三点数值例如：已知二次函数的图像过（0,0）（1,4）（-2,10） 　2020-06-14 …

如图,已知点A,B是椭圆x^2/a^2+y^2/b^2=1(a>b>0)的两个顶点,若点C(t,t 　2020-06-21 …

如果下面的DNA双螺旋从左向右进行转录,指出那条链是编码链.并写出转录产物的顺序?5’-A-T-C 　2020-06-26 …

(C/2)*K+(T/C)*F是如何换算为C=√（2T*F)/K 　2020-07-24 …

空间内两点坐标：P1（a,b,c）,P2（e,f,g）.那么,线段P1P2向量={e-a,f-b,g 　2020-12-04 …

©2023 zaojiaoba.cn 手机版 | 关于早教吧