早教吧作业答案频道 -->数学-->
如图，△ABC为钝角三角形，将△ABC绕点A按逆时针方向旋转120°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（）A、45°B、60°C、70°D、90°
题目详情
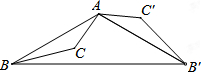如图，△ABC为钝角三角形，将△ABC绕点A按逆时针方向旋转120°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（ ）| A、45° | B、60° |
| C、70° | D、90° |
如图，△ABC为钝角三角形，将△ABC绕点A按逆时针方向旋转120°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（ ）| A、45° | B、60° |
| C、70° | D、90° |
如图，△ABC为钝角三角形，将△ABC绕点A按逆时针方向旋转120°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（ ）| A、45° | B、60° |
| C、70° | D、90° |
▼优质解答
答案和解析
考点：旋转的性质 专题：计算题 分析：先根据旋转的性质得到∠BAB′=∠CAC′=120°，AB=AB′，根据等腰三角形的性质易得∠AB′B=30°，再根据平行线的性质由AC′∥BB′得...
看了 如图，△ABC为钝角三角形，...的网友还看了以下：
不等式（2）设a,b,c＞0,求证a/(b+c)^2+b/(c+a)^2+c/(a+b)^2≥9/ 2020-06-03 …
八年级分式的运算已知a不等于b,b不等于c,c不等于a,且a/(b-c)+b/(c-a）+c/(a 2020-06-08 …
若a/(b-c)+b/(c-a)+c/(a-b)=0,求证:a/(b-c)^2+b/(c-a)^2 2020-06-12 …
M=a(b+c-a)^2+b(c+a-b)^2+c(a+b-c)^2；N=(b+c-a)(c+a- 2020-06-12 …
已知a,b,c是正数,且任意两数之和不等于第三数,根号（a+b+c）^2+根号（a-b-c)^2+ 2020-06-13 …
C语言问题#includevoidmain(){inta=3,C语言问题#includevoidm 2020-07-23 …
已知:a/b-c+b/c-a+c/a-b=0,求证:a/(b-c)^2+b/(c-a)^2+c/( 2020-07-25 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …
因式分解1、4x^2yz-12xy^2z+18xyz^22、(a-2b)^2-(3a-2b)^23、 2020-11-01 …
一道初二根号化简,已知a、b、c是一个三角形的三边长,且这个三角形的周长为24,求√（a-b-c）^ 2020-11-22 …