早教吧作业答案频道 -->物理-->
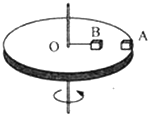
如图,圆形水平转台半径R=0.5m,上表面离水平地面的高度H=l.25m,小物块A位于转台边缘,与转台中心O距离r=0.3m的小物块B用水平细线与过O点的竖直转轴相连,A、B能随转台一起绕转轴转动,
题目详情
如图,圆形水平转台半径R=0.5m,上表面离水平地面的高度H=l.25m,小物块 A位于转台边缘,与转台中心O距离r=0.3m的小物块B用水平细线与过O点的竖直转轴相连,A、B能随转台一起绕转轴转动,当转台的角速度ω=4rad/s时,物块A刚好要滑离转台、细线断裂,此时转台立即停止转动,设物块所受的最大静摩擦力等于滑动摩擦力,小物块B与转台的动摩擦因素μB=0.1,取g=l0m/s2.求:
(1)小物块A与转台间的动摩擦因数μ;
(2)小物块B落地点离转台中心O的水平距离L.

(1)小物块A与转台间的动摩擦因数μ;
(2)小物块B落地点离转台中心O的水平距离L.
▼优质解答
答案和解析
(1)转台对物块A的静摩擦力提供物块A做圆周运动的向心力,当物块A刚要滑离转台时,转台对物块A的静摩擦力达到最大值,此时有:
μmAg=mAω2R ①
代入数据解得:μ=0.8
(2)设细线断裂时物块B的线速度大小为v0,由圆周运动的规律有:
v0=ωr ②
细线断裂后,物块B在转台上作匀减速运动,设加速度大小为a,位移为s1,滑出转台时的速度大小为v1,由牛顿第二定律有:
μBmBg=mBa ③
由几何关系有:r2+s12=R2 ④
由运动学方程有:v02-v12=2as ⑤
物块B滑离转台后在空中作平抛运动,
竖直方向上有:H=
gt2 ⑥
水平方向上有:s2=v1t ⑦
由几何关系可知:(s1+s2)2+r2=L2 ⑧
由②~⑧式可得:L=
m
答:
(1)小物块A与转台间的动摩擦因数μ是0.8;
(2)小物块B落地点离转台中心O的水平距离L是
m.
μmAg=mAω2R ①
代入数据解得:μ=0.8
(2)设细线断裂时物块B的线速度大小为v0,由圆周运动的规律有:
v0=ωr ②
细线断裂后,物块B在转台上作匀减速运动,设加速度大小为a,位移为s1,滑出转台时的速度大小为v1,由牛顿第二定律有:
μBmBg=mBa ③
由几何关系有:r2+s12=R2 ④
由运动学方程有:v02-v12=2as ⑤
物块B滑离转台后在空中作平抛运动,
竖直方向上有:H=
| 1 |
| 2 |
水平方向上有:s2=v1t ⑦
由几何关系可知:(s1+s2)2+r2=L2 ⑧
由②~⑧式可得:L=
| ||
| 10 |
答:
(1)小物块A与转台间的动摩擦因数μ是0.8;
(2)小物块B落地点离转台中心O的水平距离L是
| ||
| 10 |
看了 如图,圆形水平转台半径R=0...的网友还看了以下:
有10个村庄,坐落在从县城出发的一条公路上,相邻的距离为10km,现在准备沿路安装水管,把县城的在, 2020-03-30 …
一道汗我的数学题已知,a>0,a^2x=2√2+3,求(a^6x+a^-6x)/(a^x-a^-x 2020-05-17 …
形成电流的自由电子是怎么运动的在导体中自由电子受电场力的作用 作定向移动 我查了下 有人说是在导体 2020-05-17 …
反应较精细的功能()A.躯体ADL(PADL)B.工具性ADL(IADL)C.两者均是D.两者均不是 2020-06-07 …
结合“制作孢子印”,观察蘑菇形态图,回答问题:(1)蘑菇的地下部分是纤细的[],能够吸收外界的;地 2020-07-01 …
请各位化学高手告诉我波恩-德朗方程中德波恩指数.不要什么氦型是几,氩型是几,要特别详细的,如锌是5 2020-07-11 …
关于数列的二级递推S{n}=a{n}^2+2*a{n-1}求通项公式.{}表示下标.希望详细点,如 2020-08-01 …
当电荷瞬间接地后会产生什么情况呢?一直不清楚电荷接地后会怎么样,比如正电荷瞬间接地或负电荷瞬间接地, 2020-11-21 …
英语翻译1.在系统设计阶段,将系统功能和物流中心作业流程相结合,详细介绍了信息系统各个子系统的功能模 2020-12-14 …
这是一道初一的加减混合运算题目,详细的如下:小亮用50元钱买了10支钢笔,准备以一定的价格出售,如果 2021-02-03 …