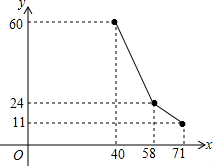
国家为支持大学生创业，提供小额无息贷款，学生王芳享受政策无息贷款36000元用来代理品牌服装的销售．已知该品牌服装进价每件40元，日销售y（件）与销售价x（元/件）之间的关系如图

Question

国家为支持大学生创业，提供小额无息贷款，学生王芳享受政策无息贷款36000元用来代理品牌服装的销售．已知该品牌服装进价每件40元，日销售y（件）与销售价x （元/件）之间的关系如图所示（实线），每天付员工的工资每人每天82元，每天应支付其它费用106元．

（1）求日销售y（件）与销售价x （元/件）之间的函数关系式；
（2）若暂不考虑还贷，当某天的销售价为48元/件时，收支恰好平衡（收入=支出），求该店员工人数；
（3）若该店只有2名员工，则该店至少需要多少天才能还清贷款，此时，每件服装的价格应定为多少元？

Answer 1

（1）当40≤x≤58时，设y与x的函数解析式为y=k₁x+b₁，由图象可得：

60=40k1+b1

24=58k1+b1

，解得：

k1=-2

b1=140

．
∴y=-2x+140；
等58<x≤71时，设y与x的函数解析式为y=k₂x+b₂，由图象得：

24=58k2+b2

11=71k2+b2

，解得：

k2=-1

b2=82

．
∴y=-x+82．
综上所述：y=

-2x+140(40≤x≤58)

-x+82(58<x≤71)

．
（2）设人数为a，当x=48时，y=-2×48+140=44，
则（48-40）×44=106+82a，
解得：a=3．
答：该店员工人数为3．
（3）令每日的收入为S元，则有：
当40≤x≤58时，S=（x-40）（-2x+140）=-2（x-55）²+450，
故当x=55时，S取得最大值450；
当58<x≤71时，S=（x-40）（-x+82）=-（x-61）²+441，
故当x=61时，S取得最大值441．
综上可知，当x=55时，S取得最大值450．
设需要b天，该店还清所有债务，则：
（450-106-82×2）b≥36000，
解得：b≥200．
故该店至少需要200天才能还清贷款，此时，每件服装的价格应定为55元．