早教吧作业答案频道 -->数学-->
已知点A、B分别在x轴,y轴上,OA=OB,点C为AB的中点,AB=122(1)如图1,求点C的坐标;(2)如图2,E、F分别为OA上的动点,且∠ECF=45°,求证:EF2=OE2+AF2;(3)在条件(2)中,若点E的坐标为(
题目详情
已知点A、B分别在x轴,y轴上,OA=OB,点C为AB的中点,AB=12
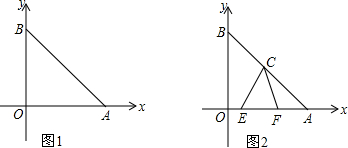
(1)如图1,求点C的坐标;
(2)如图2,E、F分别为OA上的动点,且∠ECF=45°,求证:EF2=OE2+AF2;
(3)在条件(2)中,若点E的坐标为(3,0),求CF的长.
| 2 |
(1)如图1,求点C的坐标;
(2)如图2,E、F分别为OA上的动点,且∠ECF=45°,求证:EF2=OE2+AF2;
(3)在条件(2)中,若点E的坐标为(3,0),求CF的长.

▼优质解答
答案和解析
(1)连接OC,作CM⊥OA于点M,如图1所示.
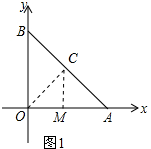
∵OA=OB,∠AOB=90°,
∴△AOB为等腰直角三角形,
∴OA=OB=12.
∵点C为线段AB的中点,
∴OC⊥AB,
∴△OCA为等腰直角三角形,
又∵CM⊥OA,
∴CM=OM=MA=
OA=6.
故点C的坐标为(6,6).
(2)证明:连接OC,在OB上截取OM=AF,连接CM、ME,如图2所示.
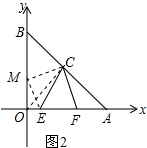
∵△AOB、△OCA、△OCB均为等腰直角三角形,
∴∠A=∠B=∠BOC=45°,OC=AC.
在△ACF和△OCM中,
,
∴△ACF≌△OCM(SAS),
∴CM=CF,∠OCM=∠ACF.
∵∠ACO=∠ACF+∠ECF+∠OCE=90°,∠ECF=45°,
∴∠ACF+∠OCE=45°=∠OCM+∠OCE=∠ECM=∠ECF.
在△ECF和△ECM中,
,
∴△ECF≌△ECM(SAS),
∴ME=EF.
在Rt△MOE中,∠MOE=90°,
∴EF2=ME2=OE2+OM2=OE2+AF2.
(3)过点C作CN⊥OA于点N,如图3所示.
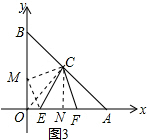
设AF=x=OM,则EF=OA-OE-AF=12-3-x=9-x=EM,
由(2)可得:(9-x)2=32+x2,
解得:x=4,
∴OF=OA-AF=12-4=8.
∵△OCA为等腰直角三角形,
∴CN=ON=
OA=6,NF=OF-ON=8-6=2.
在Rt△CNF中,∠CNF=90°,CN=6,NF=2,
∴CF=
=2
.

∵OA=OB,∠AOB=90°,
∴△AOB为等腰直角三角形,
∴OA=OB=12.
∵点C为线段AB的中点,
∴OC⊥AB,
∴△OCA为等腰直角三角形,
又∵CM⊥OA,
∴CM=OM=MA=
| 1 |
| 2 |
故点C的坐标为(6,6).
(2)证明:连接OC,在OB上截取OM=AF,连接CM、ME,如图2所示.

∵△AOB、△OCA、△OCB均为等腰直角三角形,
∴∠A=∠B=∠BOC=45°,OC=AC.
在△ACF和△OCM中,
|
∴△ACF≌△OCM(SAS),
∴CM=CF,∠OCM=∠ACF.
∵∠ACO=∠ACF+∠ECF+∠OCE=90°,∠ECF=45°,
∴∠ACF+∠OCE=45°=∠OCM+∠OCE=∠ECM=∠ECF.
在△ECF和△ECM中,
|
∴△ECF≌△ECM(SAS),
∴ME=EF.
在Rt△MOE中,∠MOE=90°,
∴EF2=ME2=OE2+OM2=OE2+AF2.
(3)过点C作CN⊥OA于点N,如图3所示.

设AF=x=OM,则EF=OA-OE-AF=12-3-x=9-x=EM,
由(2)可得:(9-x)2=32+x2,
解得:x=4,
∴OF=OA-AF=12-4=8.
∵△OCA为等腰直角三角形,
∴CN=ON=
| 1 |
| 2 |
在Rt△CNF中,∠CNF=90°,CN=6,NF=2,
∴CF=
| CN2+NF2 |
| 10 |
看了 已知点A、B分别在x轴,y轴...的网友还看了以下:
数学分析题》》关于连续的设f:D->实数,|f|:D->实数因为|f|(x)=|f(x)|举一个例 2020-06-03 …
数学分析多元函数练习问题f在闭矩阵[ab]x[cd]f对y在[cd]连续,对x在[ab](且关于y 2020-06-05 …
函数f在[a,b]的不连续点都是第一类间断点,证:f在[a,b]上有界. 2020-06-22 …
函数f在点x0存在左右导数,证f在x0连续 2020-07-31 …
1指数函数y=(1/5)^x的图象与直线y=x交点的横坐标所在的范围2若a^2>b>a>1,试比较 2020-08-01 …
若函数y=f(x)满足f(x+4)=f(x)且f(x)=f(-x),当x∈[2,3]时,f(x)= 2020-08-01 …
已知函数f:[a,b]→R(实数集合),且对于任意x,y∈[a,b],f[(x+y)/2]≤[f( 2020-08-01 …
在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在 2020-11-02 …
数学分析多元函数练习问题f在闭矩阵[ab]x[cd]f对y在[cd]连续,对x在[ab](且关于y) 2020-11-27 …
1已知函数f(x)对任意x,y∈R总有f(x)+(y)=f(x+y)且当x〉0时,f(x)〈0,f( 2020-12-03 …