早教吧作业答案频道 -->物理-->
如图甲所示,光滑绝缘斜面的倾角θ=30°,矩形区域GHIJ(GH与IJ相距为d)内存在着方向垂直于斜面的匀强磁场.质量为m、边长为d的正方形闭合金属线框abcd平放在斜面上,开始时ab边与GH相距
题目详情
如图甲所示,光滑绝缘斜面的倾角θ=30°,矩形区域GHIJ (GH与IJ相距为d)内存在着方向垂直于斜面的匀强磁场.质量为m、边长为d的正方形闭合金属线框abcd平放在斜面上,开始时ab边与GH相距也为d,现用一平行于斜面的恒力拉动线框,使其由静止开始(t=0)沿斜面向上运动,当线框完全通过磁场后运动一段时间再撤去外力.已知线框运动的过程中产生的电流I随时间t变化的 I一t图象如图乙所示(规定电流沿abcd方向为正).已知向上穿过磁场时线框中电流大小为I0,前后两次通过磁场产生电流的时间之比为2:1,重力加速度为g,斜 足够长,线框ab边始终与GH平行,求:
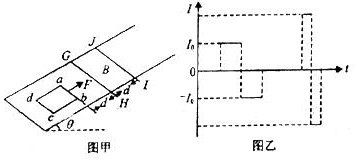
(1)匀强磁场的磁感应强度B的大小和方向;
(2)线框的电阻阻值;
(3)撤去外力之前线框位移的大小.

(1)匀强磁场的磁感应强度B的大小和方向;
(2)线框的电阻阻值;
(3)撤去外力之前线框位移的大小.
▼优质解答
答案和解析
(1)由I-t图象知道,线框向上和向下穿过磁场的过程都做匀速运动,设向上穿过磁场时线框的速度大小为v1,向下穿过磁场时线框的速度大小为v2,线框中电流大小为I;
根据运动学公式和欧姆定律可得:向上时,v1t1=2d,I0R=Bdv1;
向下时,v2t2=2d,IR=Bdv2;
根据共点力的平衡可得:mgsin30°=BId,
由题设条件知道t1:t2=2:1,
联立解得:B=
;
根据右手定则可知磁场方向垂直斜面向上;
(2)线框向上穿过磁场时.根据共点力平衡可得:
F=mgsin30°+BI0d,
线框从开始运动的ab边向上刚好进入磁场的过程中,根据动能定理可得:
(F-mgsin30°)d=
m
,
联立解得R=
;
(3)设撤去外力前位移大小为x,线框离开磁场后作用的位移为x-3d,
从线框离开磁场到再次进入磁场的过程中,根据动能定理可得:
F(x-3d)=
m
-
m
,
联立可得:x=4d.
答:(1)匀强磁场的磁感应强度B的大小为
,方向垂直斜面向上;
(2)线框的电阻阻值为
;
(3)撤去外力之前线框位移的大小为4d.
根据运动学公式和欧姆定律可得:向上时,v1t1=2d,I0R=Bdv1;
向下时,v2t2=2d,IR=Bdv2;
根据共点力的平衡可得:mgsin30°=BId,
由题设条件知道t1:t2=2:1,
联立解得:B=
| mg |
| 4I0d |
根据右手定则可知磁场方向垂直斜面向上;
(2)线框向上穿过磁场时.根据共点力平衡可得:
F=mgsin30°+BI0d,
线框从开始运动的ab边向上刚好进入磁场的过程中,根据动能定理可得:
(F-mgsin30°)d=
| 1 |
| 2 |
| v | 2 1 |
联立解得R=
mg
| ||
8
|
(3)设撤去外力前位移大小为x,线框离开磁场后作用的位移为x-3d,
从线框离开磁场到再次进入磁场的过程中,根据动能定理可得:
F(x-3d)=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
联立可得:x=4d.
答:(1)匀强磁场的磁感应强度B的大小为
| mg |
| 4I0d |
(2)线框的电阻阻值为
mg
| ||
8
|
(3)撤去外力之前线框位移的大小为4d.
看了 如图甲所示,光滑绝缘斜面的倾...的网友还看了以下:
速求,在考试中!金属A(燃烧焰色为黄色)与水反应生成气体甲与物质C,气体甲--黄绿色气体乙-》气体 2020-05-13 …
线性代数问题:A=|2 3|,B=|1 9| |-1 1| |-3 k| 若AB=BA,求k已经解 2020-05-13 …
英语作文,关于自己的改变的请结合自己的实际,谈谈进入初三之后,在生活,学习方面的变化,并谈谈为了实 2020-05-13 …
现在各种色彩鲜艳的卡通水杯深受同学们的喜爱。但是在这种卡通水杯的表面的釉质中会含有微量的Pb、Cd 2020-05-14 …
葡萄糖在肾动脉及肾静脉中的浓度试比较 葡萄糖 尿素 在肾动脉和肾静脉中的浓度,若有相异之处加以解释 2020-05-14 …
一物体从某一高度自由落下落在竖立于地面的轻质弹簧上,如图所示,在A点物体开始与轻弹簧接触,到B点时 2020-05-20 …
一种化学方面的物质.呈白色晶体状,放在嘴里有酸味,其水溶液吸热,把手放在其水溶液里感到特别凉,而且 2020-05-22 …
求老师解答:我国著名的数学家华罗我国著名的数学家华罗庚,靠自学成才.这表明[]A、分数全面反映一个 2020-06-09 …
黑洞里面的物质是以一种什么状态存在 2020-06-09 …
下面的物质哪些是岩石,哪些不是?在是的后面画对号。A石油()B大下面的物质哪些是岩石,哪些不是?在 2020-06-09 …