早教吧作业答案频道 -->数学-->
已知点A(3,0),B(0,1),以线段AB为直角边在第一象限内作等腰直角△ABC,∠BAC=90°,且点P(2,a)为平面直角坐标系中一动点.(1)请说明不论当a取何值时,△BOP的面积是一个常数.
题目详情
已知点A(3,0),B(0,1),以线段AB为直角边在第一象限内作等腰直角△ABC,∠BAC=90°,且点P(2,a)为平面直角坐标系中一动点.
(1)请说明不论当a取何值时,△BOP的面积是一个常数.
(2)要使得△ABC的面积和△ABP的面积相等,求a的值.
(1)请说明不论当a取何值时,△BOP的面积是一个常数.
(2)要使得△ABC的面积和△ABP的面积相等,求a的值.
▼优质解答
答案和解析
(1)如图,
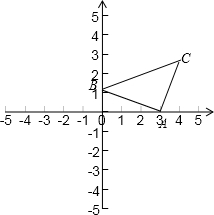
不论a取任何实数,△BOP都可以以BO=1为底,点P到y轴的距离1为高,
∴S△BOP=
×1×2=1为常数;
(2)AB=
=
,
S△ABC=
×
×
=5,
当点P在第四象限时,a<0,
∵S△ABO
×3×1=
,S△APO=-
a,
∴S△ABP=S△ABO+S△APO-S△BOP=S△ABC=5,
即
-
a-1=5,
解得a=-3,
当点P在第一象限时,同理可得a=7,
综上所述,a的值为-3或7.

不论a取任何实数,△BOP都可以以BO=1为底,点P到y轴的距离1为高,
∴S△BOP=
| 1 |
| 2 |
(2)AB=
| 12+32 |
| 10 |
S△ABC=
| 1 |
| 2 |
| 10 |
| 10 |
当点P在第四象限时,a<0,
∵S△ABO
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴S△ABP=S△ABO+S△APO-S△BOP=S△ABC=5,
即
| 3 |
| 2 |
| 3 |
| 2 |
解得a=-3,
当点P在第一象限时,同理可得a=7,
综上所述,a的值为-3或7.
看了 已知点A(3,0),B(0,...的网友还看了以下:
梯形的两条腰()A.相等B.不相等C.可以相等,也可以不相等 2020-06-13 …
“因为四边形ABCD是矩形,所以四边形ABCD的对角线相等”以上推理的大前提是()A.矩形都是四边 2020-06-13 …
下列句子中没有词类活用的一项是A.臣等以死守之B.今解鞍以示不走,用坚其意C.靳与武安君坑赵长平军 2020-07-05 …
下列关于平等的说法不正确的是()A.平等体现为人格和各项基本权利的平等B.人与人之间的平等以生命的 2020-07-17 …
在直角三角形中,两个锐角的关系是()A.互余B.互补C.相等D.以上都不在直角三角形中,两个锐角的 2020-07-20 …
有理数除法法则:除以一个不等于0的数,等于乘以这个数的.零不能做除数.两数相除,同号得,异号得.零 2020-07-30 …
下列结论中正确的是()A.在等式3a-b=3b+5的两边都除以3,可得等式a-2=b+5B.如果2= 2020-11-03 …
北京高中会考考试科目原始得分采用百分制,公布成绩使用A、B、C、D等级制.A、B、C三级为合格等级, 2020-11-06 …
下列句子中没有词类活用的一项是(3分)A.臣等以死守之B.今解鞍以示不走,用坚其意C.靳与武安君坑赵 2020-12-06 …
目前对于自然选择等问题的研究,已经从()A.个体发展到群体B.微观发展到宏观C.低等发展到高等D.以 2020-12-12 …