早教吧作业答案频道 -->数学-->
已知直线l:y=x+1与曲线C:交于不同的两点A,B,O为坐标原点.(Ⅰ)若|OA|=|OB|,求证:曲线C是一个圆;(Ⅱ)若OA⊥OB,当a>b且时,求曲线C的离心率e的取值范围.
题目详情
已知直线l:y=x+1与曲线C: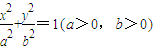 交于不同的两点A,B,O为坐标原点.
交于不同的两点A,B,O为坐标原点.
(Ⅰ)若|OA|=|OB|,求证:曲线C是一个圆;
(Ⅱ)若OA⊥OB,当a>b且 时,求曲线C的离心率e的取值范围.
时,求曲线C的离心率e的取值范围.
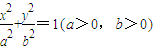 交于不同的两点A,B,O为坐标原点.
交于不同的两点A,B,O为坐标原点.(Ⅰ)若|OA|=|OB|,求证:曲线C是一个圆;
(Ⅱ)若OA⊥OB,当a>b且
 时,求曲线C的离心率e的取值范围.
时,求曲线C的离心率e的取值范围.▼优质解答
答案和解析
【答案】分析:(Ⅰ)设直线L与曲线C的交点利用两点间的距离公式和题设等式求得x12-x22=y22-y12,把A,B代入椭圆的方程两式相减求得整理求得a和b的关系,判断出曲线的图象是圆.(Ⅱ)设直线L与曲线C的交点根据a>b判断出曲线C为椭圆,根据OA⊥OB判断出两直线的斜率之积为-1,求得y1y2=-x1x2,将y=x+1代入椭圆的方程,利用韦达定理求得x1+x2和x1x2的表达式,进而利用直线方程求得y1y2的表达式,进而建立等式求得关于a和c的方程,求得a和c的关系式,进而表示出椭圆的离心率,利用a的范围确定离心率的范围.(Ⅰ)证明:设直线L与曲线C的交点为A(x1,y1)B(x2,y2)∵|OA|=|OB|∴即:x12+y12=x22+y22∴x12-x22=y22-y12∵A,B在C上∴,∴两式相减得:∴即:a2=b2∴曲线C是一个圆(Ⅱ)设直线L与曲线C的交点为A(x1,y1)B(x2,y2),∵a>b>o∴曲线C是焦点在x轴上的椭圆∵OA⊥OB∴即:y1y2=-x1x2将y=x+1代入b2x2+a2y2-a2b2=0整理得:(b2+a2)x2+2a2+a2-a2b2=0∴,∵A,B在L上∴y1y2=(x1+1)(x2+1)=x1•x2+x2+x1+1又∵y1y2=-x1x2∴2x1x2+x2+x1+1=0∴2∴b2+a2-2b2a2=0∴a2+a2-c2-2a2(a2-c2)=0∴2a4-2a2+c2-2c2a2=0∴∴∵∴2a2-1∈[2,4]∴点评:本题主要考查了直线与圆锥曲线的综合问题,椭圆的基本性质.要求考生能对椭圆中a,b和c的关系能熟练理解和应用.
看了 已知直线l:y=x+1与曲线...的网友还看了以下:
容易知道,正玄函数y=sinx是奇函数,正玄曲线关于原点对称,即原点是正玄曲线的对称中心.除原点外 2020-07-02 …
一道探索题··容易知道,正弦曲线y=sinx是奇函数,正弦曲线关于原点对称,即原点是正弦曲线的对称 2020-07-21 …
设直线关于原点对称的直线为,若与椭圆的交点为P、Q,点M为椭圆上的动点,则使△MPQ的面积为的点M 2020-07-22 …
对于抛物线y=x2与y=-x2,下列命题中错误的是()A.两条抛物线关于x轴对称B.两条抛物线关于 2020-07-26 …
关于曲线的对称性的论述正确的是()A.方程x2+xy+y2=0的曲线关于X轴对称B.方程x3+y3 2020-07-30 …
一道高三数学解析几何题双曲线X²/a²-Y²/b²=1a>0b>0离心率为根号2一条渐近线方程为L 2020-08-02 …
抛物线关于原点对称的抛物线解析式为. 2020-12-26 …
如何求一条抛物线关于原点对称得抛物线的解析式?已知一条抛物线的解析式,如何求它关于原点对称的抛物线的 2021-02-14 …
抛物线关于原点对称的抛物线解析式为. 2021-02-14 …
xy2-x2y=2x能不能通过具体的计算得出曲线关于原点对称而不是带点因为==如果是关于一条直线对称 2021-02-14 …