3世纪中期，魏晋时期的数学家刘徽首创“割圆术”，也就是在圆内割正多边形，求的近似值，刘徽容他的“割圆术”说：割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无

Question

3世纪中期，魏晋时期的数学家刘徽首创“割圆术”，也就是在圆内割正多边形，求的近似值，刘徽容他的“割圆术”说：割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失唉，当圆内接正多边形的边数无限增加时，多边形面积可无限近圆的面积，利用“割圆术”刘徽得到圆周率精确到小数点后两位的计算值3.14，这就是著名的“徽率”，如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出的n值为（参考数据：sin15°=0.259）（　　）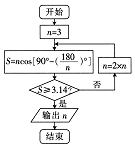

A. 6

B. 12

C. 24

D. 48

Answer 1

第1次执行循环体后，S=3cos30°=(3√(3))/(2)<3.14，不满足退出循环的条件，则n=6，
第2次执行循环体后，S=6cos60°=(1)/(2)=3<3.14，不满足退出循环的条件，则n=12，
第3次执行循环体后，S=12sin15°≈3.106<3.14，不满足退出循环的条件，则n=24，
第4次执行循环体后，S=24sin7.5°≈3.144>3.14，满足退出循环的条件，
故输出的n值为24，
故选：C．