早教吧作业答案频道 -->数学-->
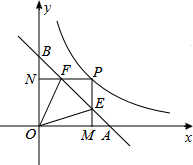
如图,直线y=-x+1交x轴于A,交y轴于B,P为反比例函数y=kx(x>0)上一点,PM⊥x轴于M,交AB于E,PN⊥y轴于N,交AB于F.若∠EOF=45°,则k的值为.
题目详情
如图,直线y=-x+1交x轴于A,交y轴于B,P为反比例函数y=
(x>0)上一点,PM⊥x轴于M,交AB于E,PN⊥y轴于N,交AB于F.若∠EOF=45°,则k的值为___.
| k |
| x |

▼优质解答
答案和解析
设P(a,b),则OM=a,PM=b,则点E的横坐标为a,F的纵坐标为b,
∵直线y=-x+1分别交x轴、y轴于A,B两点,
∴令x=0,求出y=1,即B(0,1);令y=0,求出x=1,即A(1,0),
∵OA=OB=1,且∠AOB=90°,
∴△AOB为等腰直角三角形,
∴∠FAO=∠EBO=45°,
又∵E和F都在直线y=-x+1上,
∴点E(a,1-a),点F(1-b,b),
即OM=a,EM=1-a,ON=b,NF=1-b,
∵BE=
=
a,AF=
=
b,
∵∠EOF=45°,
∴△AOF∽△BEO,
∴AF:BO=AO:BE,
∴AF•BE=BO•AO,
即
a•
b=1×1,
解得ab=
,
∴反比例函数y=
(x>0)中k的值为
.
故答案为:
.
∵直线y=-x+1分别交x轴、y轴于A,B两点,
∴令x=0,求出y=1,即B(0,1);令y=0,求出x=1,即A(1,0),
∵OA=OB=1,且∠AOB=90°,
∴△AOB为等腰直角三角形,
∴∠FAO=∠EBO=45°,
又∵E和F都在直线y=-x+1上,
∴点E(a,1-a),点F(1-b,b),
即OM=a,EM=1-a,ON=b,NF=1-b,
∵BE=
| a2+(1-1+a)2 |
| 2 |
| (1-1-b)2+b2 |
| 2 |
∵∠EOF=45°,
∴△AOF∽△BEO,
∴AF:BO=AO:BE,
∴AF•BE=BO•AO,
即
| 2 |
| 2 |
解得ab=
| 1 |
| 2 |
∴反比例函数y=
| k |
| x |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
看了如图,直线y=-x+1交x轴于...的网友还看了以下:
已知反比例函数y=k/x的图象经A(-根号3,m)过点A作AB垂直于X轴于点B且三角形的面积为根号 2020-05-15 …
与174度角终边相同的角的集合可以表示为()A.{a|a=k*180度-174度,k属于Z}B.{ 2020-05-20 …
已知映射f:A→B,其中A=B=R,对应法则f:y=e^x,对于k∈B,在集合A中都存在原象,则k 2020-05-21 …
辅音字g在i或y前的发音一般为A./K/B./g/C./d3/D./3/ 2020-07-09 …
辅音字母g在e前面的发音一般为A./k/B./g/C./tf/f去掉当中一横d./d3/ 2020-07-09 …
集合P={x|x=2k,k∈Z},Q={x|x=2k+1,k∈Z},R={x|x=4k+1,k∈Z 2020-07-30 …
如图,已知直线y=1/2x与双曲线y=k/x(k>0)交于A,B两点,且点A的横坐标为4如图,已知 2020-08-01 …
如图,已知直线y=1/2x与双曲线y=k/x(k>0)交于A.B两点,且点A的横坐标为4,不能用点 2020-08-01 …
如图,已知直线y=1/2x与双曲线y=k/x(k>0)交于A.B两点,且点A的横坐标为4如图,已知 2020-08-01 …
已知P={m/m=2k,k属于正整数,且k小于等于6},Q={n/n=6k,k属于正整数,且k小于等 2020-11-27 …