早教吧作业答案频道 -->数学-->
问题背景:如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAP=60°,探究图中线段BE、EF、FD之间的等量关系,小王同学探究此问题的方法是,延
题目详情
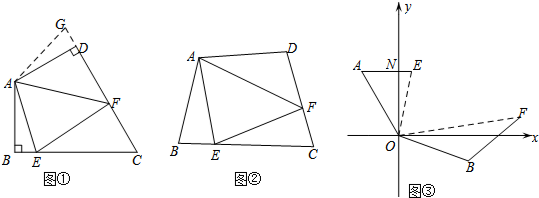
问题背景:如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAP=60°,探究图中线段BE、EF、FD之间的等量关系,小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是___.
探索延伸:如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙再指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向行驶60海里到达E处,同时舰艇乙沿北偏东50°的方向行驶100海里到达F处,此时指挥中心观测到甲、乙两舰艇之间的夹角(∠EOF)为70°,试求此时两舰艇之间的距离.
探索延伸:如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=
| 1 |
| 2 |
实际应用:如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙再指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向行驶60海里到达E处,同时舰艇乙沿北偏东50°的方向行驶100海里到达F处,此时指挥中心观测到甲、乙两舰艇之间的夹角(∠EOF)为70°,试求此时两舰艇之间的距离.

▼优质解答
答案和解析
(1)延长FD到点G.使DG=BE.连结AG,
在Rt△ABE和Rt△ADG中,
,
∴Rt△ABE≌Rt△ADG,
∴AE=AG,∠BAE=∠DAG,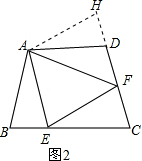
∴∠GAF=∠EAF,
在△AEF和△AGF中,
,
∴△AEF≌△AGF,
∴EF=GF,
∴EF=BE+DF;
故答案为:EF=BE+FD;
(2)成立,EF=BE+FD;
理由:延长CD至H,使DH=BE,连接AH,
∵∠B+∠ADC=180°,∠ADH+∠ADC=180°,
∴∠B=∠ADH,
在△ABE和△ADH中,
,
∴△ABE≌△ADH,
∴AE=AH,∠BAE=∠DAH,
∵∠EAF=
∠BAD,
∴∠EAF=∠HAF,
在△EAF和△HAF中,
,
∴△EAF≌△HAF,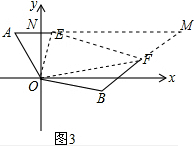
∴FH=EF,
∴EF=BE+DF,
结论运用: 如图3,连接EF,延长AE、BF交于点C,
∵∠AOB=30°+90°+(90°-70°)=140°,
∠EOF=70°,
∴∠EOF=
∠AOB,
∵OA=OB,
∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,
∴符合探索延伸中的条件
∴结论EF=AE+BF成立,
即EF=60+100=160海里,
答:此时两舰艇之间的距离是160海里.
在Rt△ABE和Rt△ADG中,
|
∴Rt△ABE≌Rt△ADG,
∴AE=AG,∠BAE=∠DAG,

∴∠GAF=∠EAF,
在△AEF和△AGF中,
|
∴△AEF≌△AGF,
∴EF=GF,
∴EF=BE+DF;
故答案为:EF=BE+FD;
(2)成立,EF=BE+FD;
理由:延长CD至H,使DH=BE,连接AH,
∵∠B+∠ADC=180°,∠ADH+∠ADC=180°,
∴∠B=∠ADH,
在△ABE和△ADH中,
|
∴△ABE≌△ADH,
∴AE=AH,∠BAE=∠DAH,
∵∠EAF=
| 1 |
| 2 |
∴∠EAF=∠HAF,
在△EAF和△HAF中,
|
∴△EAF≌△HAF,

∴FH=EF,
∴EF=BE+DF,
结论运用: 如图3,连接EF,延长AE、BF交于点C,
∵∠AOB=30°+90°+(90°-70°)=140°,
∠EOF=70°,
∴∠EOF=
| 1 |
| 2 |
∵OA=OB,
∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,
∴符合探索延伸中的条件
∴结论EF=AE+BF成立,
即EF=60+100=160海里,
答:此时两舰艇之间的距离是160海里.
看了 问题背景:如图①,在四边形A...的网友还看了以下:
引号的作用:这个洋人出的上联是“琵琶琴瑟八大王王王在上”. 2020-04-22 …
"琴瑟琵琶八大王,王王在上"的含义?快,急用啊,. 2020-06-08 …
琵琶琴瑟八大王王王在上的含义 2020-06-08 …
琴瑟琵琶八大王,王王在上,洋人出对联的用意是什么? 2020-06-08 …
“我俄人,骑奇马,张长弓,单戈成战,合手为拿,琵琶琴瑟,八大王王王在上”的下联是什么?麻烦告诉我, 2020-07-02 …
上联:骑奇马,张长弓,琴瑟琵琶八大王王王在上,单戈作战下联:伪为人,袭龙衣,魅魑魍魉四小鬼鬼鬼犯边 2020-07-02 …
骑奇马,张长纪,琵琶琴瑟八大王王王在上, 2020-07-02 …
“我俄人,骑奇马,张长弓,单戈成战,合手为拿,琵琶琴瑟,八大王王王在上”的下联是什么? 2020-07-02 …
琴瑟琵琶,八大王王王在上,单戈挑戦.下联是什么?是一个什么样的故事? 2020-07-02 …
在某个条约的签约仪式上,一个自称“中国通”的帝国主义份子写了一幅上联“琵琶琴瑟,八大王王王在上。”, 2020-12-10 …