早教吧作业答案频道 -->数学-->
如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;(1)求证:AD=BE;(2)试说明AD平分∠BAE;(3)如图2,将△CDE绕着点C旋转一
题目详情
如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;
(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.
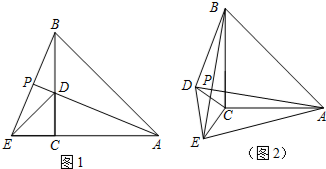
(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.

▼优质解答
答案和解析
(1)∵BC⊥AE,∠BAE=45°,
∴∠CBA=∠CAB,
∴BC=CA,
在△BCE和△ACD中,
∴△BCE≌△ACD,
∴AD=BE.
(2)∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BDP=∠ADC,
∴∠BPD=∠DCA=90°,
∵AB=AE,
∴AD平分∠BAE.
(3)AD⊥BE不发生变化.
如图2,
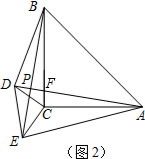
∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BFP=∠ACF,
∴∠BPF=∠ACF=90°,
∴AD⊥BE.
∴∠CBA=∠CAB,
∴BC=CA,
在△BCE和△ACD中,
|
∴△BCE≌△ACD,
∴AD=BE.
(2)∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BDP=∠ADC,
∴∠BPD=∠DCA=90°,
∵AB=AE,
∴AD平分∠BAE.
(3)AD⊥BE不发生变化.
如图2,

∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BFP=∠ACF,
∴∠BPF=∠ACF=90°,
∴AD⊥BE.
看了如图1,△ABE是等腰三角形,...的网友还看了以下:
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线 2020-04-26 …
直线AB,CD是一条河的两岸,并且AB//CD,点E为直线AB,CD外一点,现想过点E作岸CD的平 2020-05-13 …
如图,DC//AB,角BAD和角ADC的角(急)如图,DC//AB,角BAD和角ADC的角平分线相 2020-05-16 …
1.直角梯形ABCD中,AB⊥BC,DB=DC,∠DBC=50°,上底AD=6cm,求直角梯形AB 2020-06-06 …
已知AB∥CD,点E为直线AB、CD所确定的平面内一点.(1)如图1,若AE⊥AB,求证:∠C+∠ 2020-06-12 …
已知DC平行AB,角BAD和角ADC的平分线相交于点E,过点E的直线分别交DC.AB于C.B两点, 2020-06-15 …
(2013•太原)如图是我省某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A、B两点,拱 2020-07-10 …
如图,在梯形ABCD中,AB平行于DC,DB平分角ADC,过点A作AE平行BD,交CD的延长线于点 2020-07-22 …
如图是我省某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,拱桥最高点C到AB的 2020-07-22 …
如图,△ABC中,∠C=90°,D为AB中点,E、F分别在AC、BC上,且DE⊥DF.求证:AE?= 2020-11-02 …