早教吧作业答案频道 -->化学-->
(1)下列物质中,其核磁共振氢谱中给出的峰值(信号)有2个且峰的面积比为3:2的是(多选)A、B、C、D、CH3CH2CH2CH3(2)化合物A的分子式是C2H4Br2,A的核磁共振氢谱图如图,则:A的结构
题目详情
(1)下列物质中,其核磁共振氢谱中给出的峰值(信号)有2个且峰的面积比为3:2的是___(多选)
A、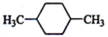 B、
B、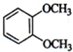 C、
C、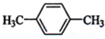 D、CH3CH2CH2CH3
D、CH3CH2CH2CH3
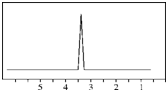
(2)化合物A的分子式是C2H4Br2,A的核磁共振氢谱图如图,则:A的结构简式为:___
(3)某烃的化学式为C4H8,其同分异构体的数目有___种(要考虑顺反异构)
(4)某化合物A 3.1g在氧气中完全燃烧,只生成4.4gCO2和2.7gH2O.则该有机物A的最简式为___,A的红外光谱表明有羟基O-H键和烃基上C-H键的红外吸收峰,而A在核磁共振氢谱中出现两组峰,且其面积之比为2:1,则该有机物的简式为___.
A、
 B、
B、 C、
C、 D、CH3CH2CH2CH3
D、CH3CH2CH2CH3(2)化合物A的分子式是C2H4Br2,A的核磁共振氢谱图如图,则:A的结构简式为:___
(3)某烃的化学式为C4H8,其同分异构体的数目有___种(要考虑顺反异构)
(4)某化合物A 3.1g在氧气中完全燃烧,只生成4.4gCO2和2.7gH2O.则该有机物A的最简式为___,A的红外光谱表明有羟基O-H键和烃基上C-H键的红外吸收峰,而A在核磁共振氢谱中出现两组峰,且其面积之比为2:1,则该有机物的简式为___.

▼优质解答
答案和解析
(1)核磁共振氢谱中给出的峰值(信号)有2个,说明有2种H原子,且峰的面积比为3:2的,即H原子个数为3:2,符合要求的有CD,A有2种H,但比值为3:4,B有3种H,故答案为:CD;
(2)化合物A的分子式是C2H4Br2,A的核磁共振氢谱图如图,说明结构对称,含有1种H,应为Br-CH2-CH2-Br,故答案为:Br-CH2-CH2-Br;
(3)C4H8且属于烯烃的有机物结构有:CH2=CHCH2CH3、CH3CH=CHCH3、CH2=C(CH3)2,其中CH3CH=CHCH3存在顺反异构,共4种,另有环丁烷、甲基环丙烷,共6种,
故答案为:6;
(4)某化合物A 3.1g在氧气中完全燃烧,只生成4.4gCO2和2.7gH2O.可知n(CO2)=
=0.1mol,n(H2O)=
=0.15mol,m(C)=1.2g,m(H)=0.3g,则m(O)=3.1g-1.2g-0.3g=1.6g,n(O)=
=0.1mol,则N(C):N(H):N(O)=0.1:0.3:0.1=1:3:1,则A的最简式为CH3O,A的红外光谱表明有羟基O-H键和烃基上C-H键的红外吸收峰,而A在核磁共振氢谱中出现两组峰,且其面积之比为2:1,则该有机物的简式为HO-CH2-CH2-OH,
故答案为:CH3O;HO-CH2-CH2-OH.
(2)化合物A的分子式是C2H4Br2,A的核磁共振氢谱图如图,说明结构对称,含有1种H,应为Br-CH2-CH2-Br,故答案为:Br-CH2-CH2-Br;
(3)C4H8且属于烯烃的有机物结构有:CH2=CHCH2CH3、CH3CH=CHCH3、CH2=C(CH3)2,其中CH3CH=CHCH3存在顺反异构,共4种,另有环丁烷、甲基环丙烷,共6种,
故答案为:6;
(4)某化合物A 3.1g在氧气中完全燃烧,只生成4.4gCO2和2.7gH2O.可知n(CO2)=
| 4.4g |
| 44g/mol |
| 2.7g |
| 18g/mol |
| 1.6g |
| 16g/mol |
故答案为:CH3O;HO-CH2-CH2-OH.
看了(1)下列物质中,其核磁共振氢...的网友还看了以下:
怎样计算标准正态分布图的面积有没有办法用辛普森法则或者梯形法则来计算给出的X在标准正态分布图上的面 2020-04-27 …
如图,已知球O的面上有四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=2,则球 2020-05-15 …
学前儿童美术教育的原则有低控制原则、发展性原则、因材施教原则、创造性原则、兴趣性原则和原则.学前儿 2020-05-16 …
农业银行客户洗钱风险等级分类的原则有哪些?( )A.全面性原则B.同一性原则C.动态管理原则D.保密 2020-05-27 …
一个吸盘,里面有一半的面积有空气,另一半没有,那么按在墙上的压力怎么算?一个吸盘,贴在墙上,靠墙部 2020-06-25 …
英语翻译该房屋交付时,上述面积为开发单位暂测面积.如该暂测面积与房地产产权登记机关实际测定的面积有 2020-06-26 …
一个圆柱形蓄水池,底面直径是6米,深是2米.要将蓄水池的侧面积和低面抹上水泥,则抹水泥的面积有多大 2020-06-30 …
建筑面积计算规则,根据建设部颁发的《建筑工程建筑面积计算规范》进行计算,那么它算出的面积有个数量其 2020-07-23 …
原始洞穴壁画的特点,新石器时代陶器表面图案的主要来源是什么,巨石结构有哪些样式?分别具体介绍.古埃 2020-08-03 …
在复杂多样、变化万千的社会生活中,我们发现,人们需要遵守各种各样的规则。大家都遵守规则,社会生活才能 2020-11-07 …