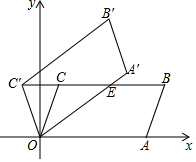
如图，在平面直角坐标系xOy中，平行四边形OABC的顶点A，B的坐标分别为（6，0），（7，3），将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′，当点C′落在BC的延长线上时，线

Question

如图，在平面直角坐标系xOy中，平行四边形OABC的顶点A，B的坐标分别为（6，0），（7，3），将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′，当点C′落在BC的延长线上时，线段OA′交BC于点E，则线段C′E的长度为___．

Answer 1

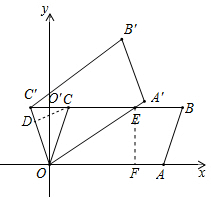∵OC=OC′，CC′⊥y轴，A，B的坐标分别为（6，0），（7，3），
∴点C到y轴的距离：7-6=1．
∴O′C=O′C′=1，O点到CC′的距离是3，
∴OC=OC′=√(10)，S_△OCC′=(1)/(2)×2×3=3．
如图，过点C作CD⊥OC′于点D，则(1)/(2)OC′•CD=3，
∴CD=(6)/(√(10))，sin∠COC′=(CD)/(OC)=(3)/(5)，tan∠COC′=(3)/(4)．
∵∠COC′+∠COE=∠AOE+∠COE，
∴∠COC′=∠AOE，
∴tan∠AOE=tan∠COC′=(3)/(4)．
如图，过E作x轴的垂线，交x轴于点F，则EF=OO'=3．
∵tan∠AOE=(EF)/(OF)，
∴OF=(EF)/(tan∠AOE)=4，
∵OF=O′E=4，
∴C′E=O′E+O′C′=4+1=5．
故答案为：5．