早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D是该抛物线的顶点.(1)求B,D两点的坐标及直线AC的解析式;(2)直线DE为这条抛物线的对称轴
题目详情
如图,在平面直角坐标系中,抛物线y=-x 2 +2x+3与x轴交于A,B两点,与y轴交于点C,点D是该抛物线的顶点.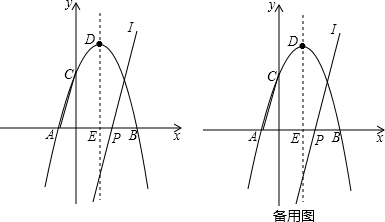
(1)求B,D两点的坐标及直线AC的解析式;
(2)直线DE为这条抛物线的对称轴,请在直线DE上找一点M,使△ACM的周长最小,求出M点的坐标;
(3)点P是x轴上的一个动点,过P点做直线l∥AC交抛物线于点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A,P,Q,C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.

(1)求B,D两点的坐标及直线AC的解析式;
(2)直线DE为这条抛物线的对称轴,请在直线DE上找一点M,使△ACM的周长最小,求出M点的坐标;
(3)点P是x轴上的一个动点,过P点做直线l∥AC交抛物线于点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A,P,Q,C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.
▼优质解答
答案和解析
考点:
二次函数综合题
专题:
压轴题
分析:
(1)令y=0,解方程求出A、B的坐标,把函数解析式整理成顶点式形式求出顶点D的坐标,再令x=0求出点C的坐标,然后利用待定系数法求一次函数解析式求解即可;(2)根据轴对称确定最短路线问题,连接BC,与对称轴的交点即为所求的点M,然后求出直线BC的解析式,再求解即可;(3)分点P在点Q的左边和右边两种情况,根据平行四边形的对边平行且相等,从点A、C的坐标关系,用点P的坐标表示出点Q的坐标,然后把点Q的坐标代入抛物线解析式求解即可.
(1)令y=0,则-x2+2x+3=0,整理得,x2-2x-3=0,解得x1=-1,x2=3,所以,点A(-1,0),B(3,0),∵y=-x2+2x+3=-(x-1)2+4,∴顶点D的坐标为(1,4),令x=0,则y=3,所以,点C的坐标为(0,3),设直线AC的解析式为y=kx+b,则-k+b=0b=3,解得k=3b=3.所以,直线AC的解析式为y=3x+3;(2)∵A、B关于对称轴直线x=1对称轴,∴直线BC与对称轴的交点即为直线DE上使△ACM的周长最小的点,设直线BC的解析式为y=mx+n,则3m+n=0n=3,解得m=-1n=3,所以,直线BC的解析式为y=-x+3,当x=1时,y=-1+3=2,所以,点M的坐标为(1,2);(3)∵直线l∥AC,∴PQ∥AC且PQ=AC,∵A(-1,0),C(0,3),∴设点P的坐标为(x,0),则①若点Q在x轴上方,则点Q的坐标为(x+1,3),此时,-(x+1)2+2(x+1)+3=3,解得x1=-1(舍去),x2=1,所以,点Q的坐标为(2,3),②若点Q在x轴下方,则点Q的坐标为(x-1,-3),此时,-(x-1)2+2(x-1)+3=-3,整理得,x2-4x-3=0,解得x1=2+7,x2=2-7,所以,点Q的坐标为(1+7,-3)或(1-7,-3),综上所述,点Q的坐标为(2,3)或(1+7,-3)或(1-7,-3).
点评:
本题是二次函数综合题型,主要考查了抛物线与x轴的交点问题,待定系数法求二次函数解析式,轴对称确定最短路线问题,平行四边形的对边平行且相等的性质,(2)确定出点M的位置是解题的关键,(3)难点在于分情况讨论.
考点:
二次函数综合题
专题:
压轴题
分析:
(1)令y=0,解方程求出A、B的坐标,把函数解析式整理成顶点式形式求出顶点D的坐标,再令x=0求出点C的坐标,然后利用待定系数法求一次函数解析式求解即可;(2)根据轴对称确定最短路线问题,连接BC,与对称轴的交点即为所求的点M,然后求出直线BC的解析式,再求解即可;(3)分点P在点Q的左边和右边两种情况,根据平行四边形的对边平行且相等,从点A、C的坐标关系,用点P的坐标表示出点Q的坐标,然后把点Q的坐标代入抛物线解析式求解即可.
(1)令y=0,则-x2+2x+3=0,整理得,x2-2x-3=0,解得x1=-1,x2=3,所以,点A(-1,0),B(3,0),∵y=-x2+2x+3=-(x-1)2+4,∴顶点D的坐标为(1,4),令x=0,则y=3,所以,点C的坐标为(0,3),设直线AC的解析式为y=kx+b,则-k+b=0b=3,解得k=3b=3.所以,直线AC的解析式为y=3x+3;(2)∵A、B关于对称轴直线x=1对称轴,∴直线BC与对称轴的交点即为直线DE上使△ACM的周长最小的点,设直线BC的解析式为y=mx+n,则3m+n=0n=3,解得m=-1n=3,所以,直线BC的解析式为y=-x+3,当x=1时,y=-1+3=2,所以,点M的坐标为(1,2);(3)∵直线l∥AC,∴PQ∥AC且PQ=AC,∵A(-1,0),C(0,3),∴设点P的坐标为(x,0),则①若点Q在x轴上方,则点Q的坐标为(x+1,3),此时,-(x+1)2+2(x+1)+3=3,解得x1=-1(舍去),x2=1,所以,点Q的坐标为(2,3),②若点Q在x轴下方,则点Q的坐标为(x-1,-3),此时,-(x-1)2+2(x-1)+3=-3,整理得,x2-4x-3=0,解得x1=2+7,x2=2-7,所以,点Q的坐标为(1+7,-3)或(1-7,-3),综上所述,点Q的坐标为(2,3)或(1+7,-3)或(1-7,-3).
点评:
本题是二次函数综合题型,主要考查了抛物线与x轴的交点问题,待定系数法求二次函数解析式,轴对称确定最短路线问题,平行四边形的对边平行且相等的性质,(2)确定出点M的位置是解题的关键,(3)难点在于分情况讨论.
看了如图,在平面直角坐标系中,抛物...的网友还看了以下:
已知一次函数y=kx+1与y=-0.5+b已知函数Y=KX+1与Y=-0.5+B的图像交于点(2, 2020-04-08 …
一次函数图像与x轴交点为(-2,0)且与正比例函数图象交于点(2,3),求这两个函数解析式 2020-04-08 …
如图,直线y=kx+b与x轴交于点(-1,0),则y<0时,x的取值范围是如图1,直线y=kx+b 2020-05-19 …
已知直线y=2x和抛物线y=ax²+3相交于点(2,b)(1)求a,b的值(2)若点A在函数y=2 2020-06-04 …
1已知函数图象与x轴交与点(-2,0)(1,0)且过点(2,8),求函数的解析式2知当x=2时,二 2020-06-27 …
已知直线L1:y=2x-1,直线L2与直线L1交于点(-2,a),且与y轴交点的坐标为7(1)L2 2020-06-27 …
已知一次函数的图像经过点(2,1)和(-1,-3)1.求此一次函数的解析式2.求此一次函数的图像与 2020-07-01 …
直线l1的方程为w=2x-1,直线l2与l1交与点(-2,a),且与y轴交与点的纵坐标为7.(1) 2020-08-02 …
已知二次函数y=ax2+bx+c的图象与轴交于点(-2,0),(x1,0),且1<x1<2,与y轴正 2020-10-31 …
已知某一次函数y=kx+b的图象经过点(0,-3),且于正比例函数y=1/2x的图象交于点(2,a) 2020-12-08 …