如图1，在四边形ABCD中，已知AB=BC=CD，∠BAD和∠CDA均为鋭角，P是对角线BD上的一点，PQ∥BA交AD于点Q，PS∥C交DC于点S，四边形PQRS是平行四边形，当点P与点B重合时，图1变为图2，若∠ABD=90°，求

Question

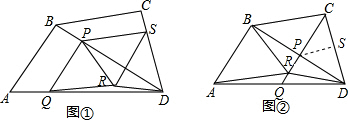
如图1，在四边形ABCD中，已知AB=BC=CD，∠BAD和∠CDA均为鋭角，P是对角线BD上的一点，PQ∥BA交AD于点Q，PS∥C交DC于点S，四边形PQRS是平行四边形，当点P与点B重合时，图1变为图2，若∠ABD=90°，求证：△ABR≌△CRD．

Answer 1

证明：∵∠ABD=90°，AB∥CR，
∴CR⊥BD．
∵BC=CD，
∴∠BCR=∠DCR．
∵四边形ABCR是平行四边形，
∴∠BCR=∠BAR．
∴∠BAR=∠DCR．
∵AB=CR，AR=BC=CD，
在△ABR和△CRD中，

AB=CR

∠BAR=∠DCR

AR=CD

，
∴△ABR≌△CRD（SAS）．