如下图所示，是树形图形.第一层是一条与水平线垂直的线段，长度为1；第二层在第一层线段的前端作两条与该段均成135°的线段，长度为其一半；第三层按第二层的方法在每一线段

Question

如下图所示，是树形图形.第一层是一条与水平线垂直的线段，长度为1；第二层在第一层线段的前端作两条与该段均成135°的线段，长度为其一半；第三层按第二层的方法在每一线段的前端生成两条线段；重复前面的做法作图至第n层.设树形图的第n层的最高点到水平线的距离为第n层树形图的高度.

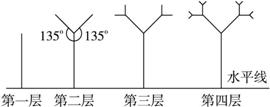
（1）求第三层及第四层树形图的高度H ₃ ，H ₄ ；

（2）求第n层树形图的高度H _n ;

（3）若树形图的高度大于2，则称树形图为“高大”，否则称为“矮小”.显然，当n=1 2时是“矮小”的，是否存在m∈Z使得当n＞m时，该树形图是“高大”的？

Answer 1

（1）设题中树（从下而上）新生的各层高度所构成的数列为{a _n }

则a ₁ =1 a ₂ = × a ₃ = a ₄ = ×

所以，第三层树形图的高度H ₃ =a ₁ +a ₂ +a ₃ =

第三层树形图的高度H ₄ =a ₁ +a ₂ +a ₃ +a ₄ =20+ .

（2）易知 ，所以第n层树形图的高度为a _n = ，

所以，当n为奇数时，第n层树形图的高度为

H _n = ;

当n为偶数时，第n层树形图的高度为

H _n =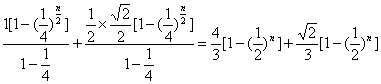

（3）不存在.由（2）知，当n为奇数时，H _n ＜

当为偶数时，H _n ＜

由定义，此树形图永远是“矮小”的.所以不存在m∈Z，使得当n＞m时，该树形图是“高大”的.