如图所示“时空之旅”飞车表演时，杂技演员架着摩托车，在球形金属网内壁上盘旋，令人惊叹不已．表演中，演员控制摩托车保持v=20m/s的速率不变，当摩托车沿最大竖直圆轨道通过金属网

Question

如图所示“时空之旅”飞车表演时，杂技演员架着摩托车，在球形金属网内壁上盘旋，令人惊叹不已．表演中，演员控制摩托车保持v=20m/s的速率不变，当摩托车沿最大竖直圆轨道通过金属网最高点A时发动机功率为零．设摩托车受到的阻力是摩托车对轨道压力的0.1倍，摩托车车身长度不计，人和车的总质量为m=200kg，取g=10m/s²，求：

（1）球形金属网的半径；
（2）摩托车沿最大竖直圆轨道通过最低点B时发动机的功率；
（3）若摩托车沿金属网内某一水平圆轨道运行时，与轨道间恰好没有侧向摩擦力，求摩托车发动机的功率．

Answer 1

解 （1）由于车在A点时的功率为0，故车在A点受到的牵引力、阻力和轨道对摩托车的弹力均为0．由牛顿运动定律得：mg=(mv2)/(R)代入数据解得：R=(v2)/(g)=(202)/(10)m=40m
（2）设摩托车在最低点B点时，轨道对它的弹力为N_B，由牛顿运动定律得：
 N_B-mg=(mv2)/(R)解得：N_B=(mv2)/(R)+mg=200×(202)/(40)+200×10=4000N
摩托车在B点时受到的阻力为：f=kN=0.1×4000N=400N
则发动机的牵引力为：F=f=400N
故摩托车在B点时的功率为：P=Fv=400×20W=8000W
（3）设摩托车所在圆的切线与水平面夹θ角，摩托车受重力、支持力、摩擦力，
则  N=(mg)/(cosθ)  Nsinθ=m(v2)/(r)    r=Rsinθ  f=0.1N    p=fv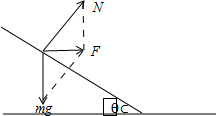
代入数据联立解得  p=2000（√(5)+1）=6470W
答：
（1）竖直圆轨道的半径为40m．
（2）摩托车通过最低点B时发动机的功率为8000W
（3）摩托车发动机的功率6470W．