早教吧作业答案频道 -->物理-->
云霄飞车是迪士尼游乐项目之一,其实就是一种过山车,为明白其原理特简化成以下模型:如图所示轨道在竖直面内,由倾斜、圆形、水平三部分组成,其中圆形部分两边的是圆环,中间的
题目详情
云霄飞车是迪士尼游乐项目之一,其实就是一种过山车,为明白其原理特简化成以下模型:如图所示轨道在竖直面内,由倾斜、圆形、水平三部分组成,其中圆形部分两边的是圆环,中间的是圆管,B、C、D分别是轨道的三个圆形部分的最低点,B、C间距与C、D间距相等,轨道倾斜、圆形部摩擦不计,飞车与轨道的水平部分间的动摩擦因数μ=0.2,半径R1=2.0m、R2=3.0m,整个轨道装置的质量M=4kg,固定在地面上.质量为m=2.0kg的飞车(视为质点,轨道圆管部分的直径比飞车高度略大)从轨道的左侧A点静止滑下,当飞车运动到轨道的第一个圆形部分的最高点时,整个轨道对地刚好无压力,且飞车恰好能过轨道的第二、三个图形部分的最高点.假设水平轨道足够长,轨道的圆形间不互相重叠.重力加速度取g=10m/s2.试求:
(1)飞车出发位置到轨道最低点的高度;
(2)B、C间距应是多少?
(3)轨道的第三个圆形部分的半径R3是多少;飞车最终停留点与D点的距离.
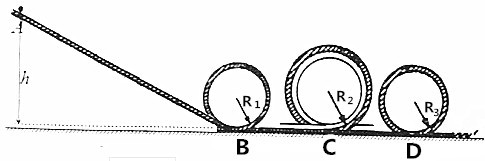
(1)飞车出发位置到轨道最低点的高度;
(2)B、C间距应是多少?
(3)轨道的第三个圆形部分的半径R3是多少;飞车最终停留点与D点的距离.

▼优质解答
答案和解析
(1)要使飞车到达轨道的第一个圆形部分的最高点时,整个轨道对地刚好无压力,则说明飞车对轨道向上的压力为FN=Mg=4×10=40N; 则可知轨道对飞车由向下的40N的压力; 由向心力公式可知:
mg+FN′=m
对飞车由最高点下滑到第一个轨道的最高点过程由机械能守恒定律可知:
mg(h-2R1)=
mv12
联立解得:h=7m;
(2)飞车恰能通过第二个圆轨道的最高点,则有:
v2=0;
对从最高点至到达第二个轨道的最高点,由动能定理可知:
mg(h-2R2)-μmgs=
mv22;
联立解得:s=0.5m;
(3)飞车通过最后一个圆形最高点时,根据向心力公式有:
mg=m
对从第二个轨道的最高点到三个轨道的最高点,由动能定理可知:
mg(2R2-2R3)-μmgs=
mv32
解得:R3=2.36m;
对第三个轨道的最高点到最终停止过程,由动能定理可知:
μmgx=
mv32
解得:x=0.59m;
答:(1)飞车出发位置到轨道最低点的高度7m;
(2)B、C间距应是0.5m;
(3)轨道的第三个圆形部分的半径R3是2.36m;飞车最终停留点与D点的距离0.59m
mg+FN′=m
| ||
| R1 |
对飞车由最高点下滑到第一个轨道的最高点过程由机械能守恒定律可知:
mg(h-2R1)=
| 1 |
| 2 |
联立解得:h=7m;
(2)飞车恰能通过第二个圆轨道的最高点,则有:
v2=0;
对从最高点至到达第二个轨道的最高点,由动能定理可知:
mg(h-2R2)-μmgs=
| 1 |
| 2 |
联立解得:s=0.5m;
(3)飞车通过最后一个圆形最高点时,根据向心力公式有:
mg=m
| ||
| R3 |
对从第二个轨道的最高点到三个轨道的最高点,由动能定理可知:
mg(2R2-2R3)-μmgs=
| 1 |
| 2 |
解得:R3=2.36m;
对第三个轨道的最高点到最终停止过程,由动能定理可知:
μmgx=
| 1 |
| 2 |
解得:x=0.59m;
答:(1)飞车出发位置到轨道最低点的高度7m;
(2)B、C间距应是0.5m;
(3)轨道的第三个圆形部分的半径R3是2.36m;飞车最终停留点与D点的距离0.59m
看了云霄飞车是迪士尼游乐项目之一,...的网友还看了以下:
郭斌铄教授曾这样评价一位中国近代思想家:“先生于中西治术学理,实能究极源委,有以探其异同得失之所在 2020-04-06 …
祖茂,武昌太守.潜少怀高尚,博学善文,颖脱不羁,任真自得,以乡邻之所贵.其亲朋好事,或载酒肴而往, 2020-04-27 …
“明主之所制其臣者,二柄而已矣.二柄者,刑德也.何谓刑德?曰:杀戮之谓刑,庆赏之谓德.”材料对“刑 2020-06-17 …
您对:“邪之所凑,其气必虚,阴虚者,阳必凑之!”有什么不同解释?“邪之所凑,其气必虚,阴虚者,阳必 2020-06-20 …
英语翻译祸兮福之所倚.福兮祸之所伏.孰知其极,其无正邪?正复为奇,善复为妖.人之所迷,其日固久. 2020-06-23 …
英语翻译王凤等乞降,不许.寻、邑自以为功在漏刻,意气甚逸.夜有流星坠营中,昼有?气如坏山,当营而陨 2020-07-10 …
想人之所想及人之所及其中“及”字怎么解释 2020-07-14 …
对下列各句句式特点归类正确的一项是(2分)()①函谷举②不吾知也③而为秦人积威之所劫④其又何尤⑤方其 2020-11-11 …
英语翻译"方春兴作,则粟宜贵之时,因其不足而出粟以资之.方秋收成,则粟宜贱之时,因其有余而敛之.如此 2020-11-22 …
而后向之所云诸景,若舍塞而就旷,却晦而即明。翻译 2020-12-17 …