早教吧作业答案频道 -->数学-->
未来一年,重庆将在打造“森林重庆”的过程中对“两翼一圈”中的“两翼”地区实施万元增收工程,为了提高农户收入,某县决定对在森林间的空地上种植中草药实行政府补贴,规定
题目详情
未来一年,重庆将在打造“森林重庆”的过程中对“两翼一圈”中的“两翼”地区实施万元增收工程,为了提高农户收入,某县决定对在森林间的空地上种植中草药实行政府补贴,规定每种植一亩中草药一次性补贴农户若干元,经调查,种植亩数y(亩)与补贴数额x(元)之间成一次函数关系,且补贴与种植情况如下表:
随着补贴数额x的不断增大,种植规模也不断增加,但每亩中草药的收益z(元)会相应降低,该县补贴政策实施前每亩中草药的收益为3000元,而每补贴10元,每亩中草药的收益会相应减少30元.
(1)分别求出政府补贴政策实施后,种植亩数y(亩)、每亩中草药的收益z(元)与政府补贴数额x(元)之间的函数关系式;
(2)要使全县种植这种中草药的总收益W(元)最大,政府应将每亩补贴数额x定为多少元?并求出总收益W的最大值和此时的种植亩数:(总收益=每亩收益×亩数)
(3)在取得最大收益的情况下,为了发展森林旅游,需占用其中不超过60亩的森林间空地修建一个森林公园.已知修建森林公园平均每亩的费用为650元,此外还要购置部分游乐设施,这项费用(元)等于空地面积(亩)的平方的25倍.这样,将空地用来修建森林公园比用来种植中草药时每亩的平均收益增加了2000元,在扣除所有修建费用后总收益为85000元,求修建的森林公元有多少亩?(精确到个位)(参考数据: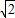 =1.414,
=1.414,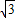 =1.732,
=1.732,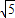 =2.236)
=2.236)
| 补贴数额x(元) | 100 | 200 | … |
| 种植亩数y(亩) | 1600 | 2400 | … |
(1)分别求出政府补贴政策实施后,种植亩数y(亩)、每亩中草药的收益z(元)与政府补贴数额x(元)之间的函数关系式;
(2)要使全县种植这种中草药的总收益W(元)最大,政府应将每亩补贴数额x定为多少元?并求出总收益W的最大值和此时的种植亩数:(总收益=每亩收益×亩数)
(3)在取得最大收益的情况下,为了发展森林旅游,需占用其中不超过60亩的森林间空地修建一个森林公园.已知修建森林公园平均每亩的费用为650元,此外还要购置部分游乐设施,这项费用(元)等于空地面积(亩)的平方的25倍.这样,将空地用来修建森林公园比用来种植中草药时每亩的平均收益增加了2000元,在扣除所有修建费用后总收益为85000元,求修建的森林公元有多少亩?(精确到个位)(参考数据:
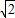 =1.414,
=1.414,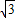 =1.732,
=1.732,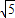 =2.236)
=2.236)▼优质解答
答案和解析
分析:
(1)根据图表提供的数据,可用待定系数法,分别求出种植亩数y、每亩蔬菜的收益z与政府补贴数额x之间的一次函数关系式;(2)根据(1)中z与x,以及y与x之间的关系,可以求出w与x之间的二次函数关系式,再根据二次函数最值公式求出即可;(3)设修建了s亩蔬菜大棚,根据题意列方程解出s值.
(1)设y=kx+b,由图表将点(100,1600),(200,2400),代入得,1600=k×100+b,2400=k×200+b,解得:k=8,b=800,∴y=8x+800,同理:设z=mx+n,由题意可得n=3000,将点(100,2700),代入z=mx+3000,2700=m×100+3000,解得:m=-3,∴z=-3x+3000;(2)∵w=yz=(8x+800)(-3x+3000)=-24x2+21600x+2400000,∴w=-24(x-450)2+7260000,∴每亩应补贴x=450元,w的最大值为7260000元,此时,y=8×450+800=4400亩;(3)设修建了s亩蔬菜大棚,原来每亩的平均收益为=1650元,由题意得方程:(1650+2000)s-650s-25s2=85000,解得s1=60+10≈74,s2=60-10≈46,∵0<s≤60,∴s≈46.答:修建了46亩蔬菜大棚.
点评:
本题主要考查了二次函数的性质在实际生活中的应用,读懂题意,认真分析表示出各部分建筑费,找到等量关系列出方程是解决问题的关键.
分析:
(1)根据图表提供的数据,可用待定系数法,分别求出种植亩数y、每亩蔬菜的收益z与政府补贴数额x之间的一次函数关系式;(2)根据(1)中z与x,以及y与x之间的关系,可以求出w与x之间的二次函数关系式,再根据二次函数最值公式求出即可;(3)设修建了s亩蔬菜大棚,根据题意列方程解出s值.
(1)设y=kx+b,由图表将点(100,1600),(200,2400),代入得,1600=k×100+b,2400=k×200+b,解得:k=8,b=800,∴y=8x+800,同理:设z=mx+n,由题意可得n=3000,将点(100,2700),代入z=mx+3000,2700=m×100+3000,解得:m=-3,∴z=-3x+3000;(2)∵w=yz=(8x+800)(-3x+3000)=-24x2+21600x+2400000,∴w=-24(x-450)2+7260000,∴每亩应补贴x=450元,w的最大值为7260000元,此时,y=8×450+800=4400亩;(3)设修建了s亩蔬菜大棚,原来每亩的平均收益为=1650元,由题意得方程:(1650+2000)s-650s-25s2=85000,解得s1=60+10≈74,s2=60-10≈46,∵0<s≤60,∴s≈46.答:修建了46亩蔬菜大棚.
点评:
本题主要考查了二次函数的性质在实际生活中的应用,读懂题意,认真分析表示出各部分建筑费,找到等量关系列出方程是解决问题的关键.
看了未来一年,重庆将在打造“森林重...的网友还看了以下:
.连续出现有什么作用?前面没位置打了.“森林后面还是森林,再望过去,还是森林,望的更远还是森林,森 2020-05-13 …
从古猿到人类形态变化的过程中,你认为起根本作用的是什么?不要回答这个:最佳答案由于声林森林大量消失 2020-05-16 …
翻译过马路时,要环顾四周.这条马路穿过森林.翻译过马路时,要环顾四周.这条马路穿过森林.在茶室里, 2020-06-21 …
上联:木林森森林木.请回答下联单木为木二木为林,三木可成森林,森林茂盛成森密,木经积聚由少而多终成 2020-06-27 …
为何东北原始森林中的树种多是针叶林和小阔叶林与我过其他地方的森林有甚么不同 2020-07-21 …
2015年1月8日,上海市高级人民法院对复旦学生林森浩投毒案二审公开审判:驳回上诉,维持原判.一审判 2020-12-05 …
英语翻译深邃深邃的森林里,吹过清凉的风.穿透树叶的日光,轻轻地映村你安详的面庞.这片森林中的你,永远 2020-12-06 …
森林林冠对降水的截流一般为15%-30%,林下藓苔,枯枝落叶对降水可再次截流,并且森林土壤具有较高的 2021-01-06 …
森林林冠对降水的截流一般为15%-30%,林下藓苔,枯枝落叶对降水可再次截流,并且森林土壤具有较高的 2021-01-06 …
根据下面一句话,展开自己的想象,写一篇自己喜欢的300字左右的小作文。自己加一个题目。一场森林大火过 2021-01-12 …