本题为分叉题。A组适用于《生物》教材，B组适用于《生命科学》教材，A组和B组中任选做一题，两组都做以A给分。A组材料1：1642年，比利时科学家海尔蒙特进行了一项著名的柳

Question

本题为分叉题。A组适用于《生物》教材，B组适用于《生命科学》教材，A组和B组中任选做一题，两组都做以A给分。

A组   材料1：1642年，比利时科学家海尔蒙特进行了一项著名的柳树实验。他在一个花盆里栽种了一棵2.3kg的柳树。栽种前，花盆里的泥土经过高温烘烤干燥后称重为90.8kg。以后的5年中，海尔蒙特除了只给柳树浇水外，没有在花盆里添加任何物质，每年秋天柳树的落叶也没有称重和计算。5年后，他将柳树和泥土分开称重，发现柳树的重量变成了76.7kg，泥土烘干后的重量为90.7kg，比原来只减少0.1kg。于是他得出结论：柳树获得的74.4kg物质只是来源于水。

材料2：科学家将一盆绿色植物放在不同波长的光下照射，然后测量该植物对不同光质的吸光率，结果如下：

光质	红    橙   黄    绿    青   蓝   紫
波长（nm） 吸光率（%）	700  650  600   550   500  450  400 55    10    2    1     5    85   40

（1）根据你所学的生物学知识，判断海尔蒙特的结论是否确切？为什么？           。

（2）花盆内的泥土减少了0.1kg，其原因是                                         。

（3）请用表中数据在下方格纸内绘出植物叶片光吸收变化曲线，并分析得出的结论                                                                          

                                                                    。

  

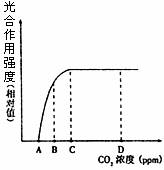
（4）二氧化碳浓度对植物光合作用强度影响的规律如上右图。当外界二氧化碳浓度处于A时，植物叶片光合作用所固定的CO ₂ 量与             相等；为提高封闭大棚内作物产量，棚内人工释放CO ₂ 应控制在             （填图中字母）浓度为宜。

B组   Mikael为了探究光照强度和光合作用速率的关系，以便为西红柿生长提供最佳光照强度。实验如下：实验过程：他取几株都有5片叶片的西红柿植株，分别放在密闭的玻璃容器中。实验开始他测定了CO ₂ 的浓度，12小时后再次测定CO ₂ 的浓度。他还采用7种不同的光照强度，并通过隔热装置使光线通过而热不通过。

实验结果：

温度℃	光照强度：普通阳光（%）	开始时的CO 2 浓度（%）	12小时后 CO 2 浓度（%）
25	0	0.35	0.368
25	10	0.35	0.342
25	20	0.35	0.306
25	40	0.35	0.289
25	60	0.35	0.282
25	80	0.35	0.280
25	95	0.35	0.279

请你据此分析回答下列问题：

（1）这一实验的自变量是什么？                                           。说出该实验中的一种控制变量                                。

（2）Mikael设计的探究实验在各种光照强度变化中分别使用了不同株植物。这是一个好的设计吗？             为什么？                                               。

（3）在这一实验中Mikael将其中一个装置保持在黑暗中的目的是                       。

（4）Mikael对探究结果感到失望。他说，“我仍然不能确切地知道哪种光照强度最好？”请你为他的进一步探究提供建议                                                。

 （5）Mikael要用曲线图表示他的实验结果。怎样最好地图示结果？（在四项备选项中选择）             。

       A．柱形图，12小时后的二氧化碳浓度和光照强度分别为纵坐标和横坐标

       B．柱形图，开始时的二氧化碳浓度和光照强度分别为纵坐标和横坐标

       C．曲线图，12小时后的二氧化碳浓度和光照强度分别为纵坐标和横坐标

       D．曲线图，开始时的二氧化碳浓度和光照强度分别为纵坐标和横坐标

Answer 1

A组（1）不确切。植物吸收的水分主要用于蒸腾作用，只有少量的水分参与光合作用；柳树重量的增加主要来自于光合作用合成的有机物（柳树重量的增加主要来自空气中的二氧化碳）（2分） （2）柳树生长过程从...