如图所示，传送带的右边平滑对接倾角为30°的光滑固定的斜面，左边对接固定的挡板，传送带ab的长度l=2.0m，它始终以v=3.0m/s的速度顺时针转动．现将一个可视为质点的小物体由c点静止释放

Question

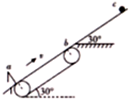
如图所示，传送带的右边平滑对接倾角为30°的光滑固定的斜面，左边对接固定的挡板，传送带ab的长度l=2.0m，它始终以v=3.0m/s的速度顺时针转动．现将一个可视为质点的小物体由c点静止释放，bc距离L=1.4m，小物体与传送带表面的动摩擦因数μ=(√(3))/(2)，取g=10m/s²．求：

（1）小物体运动到传送带的下端a点时的速率；
（2）若小物体与挡板相撞时无机械能损失，试通过计算说明小物体能否与挡板发生第二次相撞．

Answer 1

（1）物体在bc段运动时的加速度为a₁，由牛顿第二定律得
  mgsin30°=ma₁，解得 a₁=5m/s²；
滑到b点的速度 v₁=√(2×5×1.4)=√(14)m/s
物体在ab段运动时的加速度为a₂，由牛顿第二定律得
  mgsin30°-μmgcos30°=ma₂，解得 a₂=-2.5m/s²；
所以，物体撞击挡板时的速率为v₂，则有

v

2 2

-

v

2 1

=2a₂l
解得 v₂=2m/s
（2）物体反弹后沿传送带向上做匀加速运动，其加速度大小为 a₃．
根据牛顿第二定律得
  μmgcos30°-mgsin30°=ma₃，解得 a₃=2.5m/s²；
物体匀加速运动的位移 x₁=(v2-v22)/(2a3)=1m
由于 x₁<l，所以物体在传送带上先匀加速后匀速，物体从b点以3m/s的速率向上运动，又以3m/s的速率向下运动滑上传送带，物体在传送带上向下滑动的最大位移为
  x₂=(v2)/(2a2)=(32)/(2×1.5)=1.8m
因为 x₂<l，所以小物体不能与挡板发生第二次相撞．
答：
（1）小物体运动到传送带的下端a点时的速率是2m/s．
（2）小物体不能与挡板发生第二次相撞．