函数f（x）=[x]-x（函数y=[x]的函数值表示不超过x的最大整数，如（[-3.6]=-4，[2.1]=2），设函数g（x）=f(x)+lgx(x>0)f(x)-sinx(-2π<x<0)，则函数y=g（x）的零点的个数为（）A.11B.10C.12D.13

Question

函数f（x）=[x]-x（函数y=[x]的函数值表示不超过x的最大整数，如（[-3.6]=-4，[2.1]=2），设函数g（x）=

f(x)+lgx(x>0)

f(x)-sinx(-2π<x<0)

，则函数y=g（x）的零点的个数为（　　）

A. 11

B. 10

C. 12

D. 13

Answer 1

①当x>0时，f（x）=[x]-x，当0当1≤x<2时，f（x）=1-x；…，当10≤x<11时，f（x）=10-x；…，
当11≤x<12时，f（x）=11-x；…．函数y=-lgx，（x>0）．
因此；当00，
此时函数g（x）无零点；当1≤x≤10时，
0≥-lgx≥-1，此时函数g（x）有9个零点；
当10此时函数g（x）无零点．
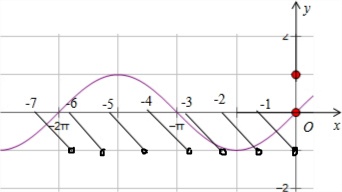
②当x<0时，f（x）=[x]-x，
当-1≤x<0时，f（x）=-1-x；
当-2≤x<-1时，f（x）=-2-x；…，
当-6≤x<-5时，f（x）=-6-x；当-2π函数y=sinx，（x>0）．如图所示：此时函数g（x）有3个零点．
综上可得：函数g（x）共有12个零点．
故选：C．