车站、码头、机场等使用的货物安检装置的示意图如图所示，绷紧的传送带始终保持v=1m/s的恒定速率运行，AB为传送带水平部分且长度L=2m，现有一质量为m=1kg的背包（可视为质点）无初速度

Question

车站、码头、机场等使用的货物安检装置的示意图如图所示，绷紧的传送带始终保持v=1m/s的恒定速率运行，AB为传送带水平部分且长度L=2m，现有一质量为m=1kg的背包（可视为质点）无初速度的放在水平传送带的A端，传送到B端时没有被及时取下，背包从B端沿倾角为37°的斜面滑入储物槽，已知背包与传送带的动摩擦因数μ₁=0.5，背包与斜面间的动摩擦因数μ₂=0.8，不计空气阻力（g=10m/s²，sin37°=0.6，cos37°=0.8）．求：

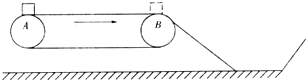
（1）背包对于传送带的相对位移的大小；
（2）由于放了背包，带动传送带的电动机多消耗的电能；
（3）若B轮的半径为R=0.2m，求背包运动到B点时对传送带的压力的大小；
（4）为了减少对背包的损害，要求背包滑到储物槽时的速度刚好为零，求斜面的长度．

Answer 1

（1）背包在水平传送带上由滑动摩擦力产生加速度，由牛顿第二定律得 μ₁mg=ma₁．
背包达到传送带的速度所用时间 t₁=(v)/(a1)=(v)/(μ1g)=(1)/(0.5×10)=0.2s
背包达到传送带的速度时对地位移 x₁=(1)/(2)a1

t

2 1

联立解得 x₁=0.1m<L=2m
共速后背包与传送带相对静止，没有相对位移，所以背包对于传送带的相对位移为△x=vt₁-x₁=1×0.2-0.1=0.1m
（2）背包和传送带间的摩擦生热 Q=μ₁mg△x
背包获得的动能 E_k=(1)/(2)mv2
所以电动机多消耗的电能为 E=Q+E_k．
解得 E=1J
（3）背包在B点受到重力和支持力的作用，由牛顿第二定律得
   mg-N=m(v2)/(R)
解得 N=5N
根据牛顿第三定律知：背包对传送带的压力大小 N′=N=5N，方向竖直向下．
（4）背包在斜面上受到重力、支持力和滑动摩擦力，沿斜面向下做匀减速直线运动，由牛顿第二定律得
    μ₂mgcos37°-mgsin37°=ma₂．
要使它到达底端时的速度恰好为0，则有 0-v²=-2a₂x
解得 x=1.25m
所以斜面的长度是1.25m．
答：
（1）背包对于传送带的相对位移的大小是0.1m；
（2）由于放了背包，带动传送带的电动机多消耗的电能是1J；
（3）若B轮的半径为R=0.2m，求背包运动到B点时对传送带的压力的大小是5N；
（4）为了减少对背包的损害，要求背包滑到储物槽时的速度刚好为零，斜面的长度是1.25m．