情景：校园空地上有一残墙，现有长为48米的塑胶铁丝网，再利用这面残墙围成一个矩形花圃．问题：（1）填空：当残墙为12米时，所围矩形花圃的最大面积是m2当残墙为20米时，所围矩形

Question

情景：
校园空地上有一残墙，现有长为48米的塑胶铁丝网，再利用这面残墙围成一个矩形花圃．
问题：
（1）填空：当残墙为12米时，所围矩形花圃的最大面积是___m²
当残墙为20米时，所围矩形花圃的最大面积是___m²
当残墙为28米时，所围矩形花圃的最大面积是___m²
（2）当残墙为a米时，设所围矩形花圃的最大面积为 S平方米，请写出S 与a的函数关系，并写出a的取值范围．
（3）当残墙足够长时，设靠墙的一面的矩形长为x米，矩形花圃的面积为y平方米，请写出y与x的函数关系．
（4）若残墙a=14米时，设靠墙的一面的矩形长为x米，矩形花圃的面积为y平方米，当84≤y≤238时，求x的取值范围．

Answer 1

（1）设矩形花圃的面积为y，BC长为xm，则AB长为(1)/(2)（48-2）m．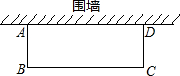
依题意，得y=(1)/(2)x（48-x）=-(1)/(2)（x-24）²+288．
∴抛物线的对称轴方程为x=24．
∵a=-(1)/(2)<0，
∴当x<24时，y随x的增大而增大．
当残墙为12米时，所围矩形花圃的最大面积=-(1)/(2)(12-24)2+288=216；
当残墙为20米时，所围矩形花圃的最大面积=-(1)/(2)(20-24)2+288=280；
当残墙为28米时，x=24，所围矩形花圃的最大面积=288；
∴当x=12m时，S_最大=144m²，
故答案为：216；280；288；
（2）由（1）可知，当a≥24时，S=288m²；
当0<a<24时，S=-(1)/(2)(a-24)2+288；
（3）设AB=x，则BC=48-2x．
由矩形的面积公式得：y=（48-2x）x=-2（x-12）²+288；
（4）∵a=14，
∴48-2x≤14．
∴x≥17．
∵84≤y≤238，
∴

-2(x-12)2+288≥84①

-2(x-12)2≤238②

解得：19≤x≤22．
∴x的取值范围是：19≤x≤22．