早教吧作业答案频道 -->数学-->
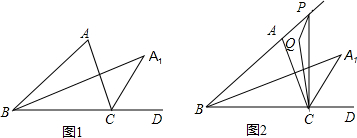
如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1,(1)当∠A为70°时,则∠A1的度数是°;当∠A=90°时,∠A1的度数是°;(2)①探索∠A与∠A1之间数量关系并
题目详情
如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1,
(1)当∠A为70°时,则∠A1的度数是___°;当∠A=90°时,∠A1的度数是___°;
(2)①探索∠A与∠A1之间数量关系并证明你的结论;
②若∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请你直接写出∠An与∠A的数量关系___;
(3)如图,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,随着点P的运动,∠Q+∠A1的值是否变化?若变化,请说名理由;若不变,请求出其值.
(1)当∠A为70°时,则∠A1的度数是___°;当∠A=90°时,∠A1的度数是___°;
(2)①探索∠A与∠A1之间数量关系并证明你的结论;
②若∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请你直接写出∠An与∠A的数量关系___;
(3)如图,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,随着点P的运动,∠Q+∠A1的值是否变化?若变化,请说名理由;若不变,请求出其值.

▼优质解答
答案和解析
(1)∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=
∠ABC,∠A1CD=
∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴
(∠A+∠ABC)=
∠ABC+∠A1,
∴∠A1=
∠A,
∵∠A=70°,
∴∠A1=35°
∵∠A=90°,
∴∠A1=45°;
故答案为:35,45;
(2)①∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=
∠ABC,∠A1CD=
∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴
(∠A+∠ABC)=
∠ABC+∠A1,
∴∠A1=
∠A;
②同②可求得:
∠A2=
∠A1=
∠A,
∠A3=
∠A2=
∠A,
…
依此类推,∠An=
∠A;
故答案为:∠An=
∠A;
(3)△ABC中,由三角形的外角性质知:∠BAC=∠AEC+∠ACE=2(∠QEC+∠QCE);
即:2∠A1=2(180°-∠Q),
化简得:∠A1+∠Q=180°.
∴∠A1BC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠A1=
| 1 |
| 2 |
∵∠A=70°,
∴∠A1=35°
∵∠A=90°,
∴∠A1=45°;
故答案为:35,45;
(2)①∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠A1=
| 1 |
| 2 |
②同②可求得:
∠A2=
| 1 |
| 2 |
| 1 |
| 22 |
∠A3=
| 1 |
| 2 |
| 1 |
| 23 |
…
依此类推,∠An=
| 1 |
| 2n |
故答案为:∠An=
| 1 |
| 2n |
(3)△ABC中,由三角形的外角性质知:∠BAC=∠AEC+∠ACE=2(∠QEC+∠QCE);
即:2∠A1=2(180°-∠Q),
化简得:∠A1+∠Q=180°.
看了如图,△ABC中,∠ABC的角...的网友还看了以下:
已知3/2X²-2a=0的一个根,则2a-1的值是()A.3 B.4 C.5 D.6方程X²-3X 2020-05-16 …
反向购买问题A上市公司发行新股用来交换公司B的全部股权,交换后,B公司的原股东持有公司A公司90% 2020-06-25 …
有如下算法描述①输入整数a②如果a是奇数转到⑥③如果a是偶数转到⑤④将a的值相乘以后赋给a⑤将a的 2020-07-24 …
当a是正数时,-a是();当a是0时,-a是(),当a是负数时,-a是().所以-a()是负数. 2020-07-30 …
1.若关于x的分式方程4x/x-5=a/5-x-1有增根,那么增根是,这时a=?2.已知x-1/x 2020-07-31 …
(2011•荆门)请根据图中a、b、c三种物质的溶解度曲线,回答下列问题:(1)P点的含义是t1℃时 2020-11-12 …
关于函数对称变换的一些问题、有兴趣的来讨论一下吧!函数对称变换中有一个公式:y=f(a-x)与y=f 2020-11-20 …
填空题:1.一个圆的半径为r,是另一个圆的半径的3倍,这两个圆的周长之和是.2.若(x+3)(x-5 2020-12-05 …
a,b,c是三个不同的自然数,根据a除b=c,a的因数至少有()个,当a和c的最大公因数是1时a,b 2021-01-05 …
a是正数,-a就表示();当A是0时,-A就表示()2,在乒乓球比赛中,71班胜了-4场,输了-1场 2021-02-04 …