早教吧作业答案频道 -->数学-->
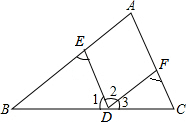
小学里我们已经学过三角形的三个内角和等于180°,下面是一种证明∠A+∠B+∠C=180°的方法,请完成说理过程(填空):如图,在三角形ABC的一边BC上取一点D,DE∥AC,DF∥AB.(为说理方
题目详情
小学里我们已经学过三角形的三个内角和等于180°,下面是一种证明∠A+∠B+∠C=180°的方法,请完成说理过程(填空):如图,在三角形ABC的一边BC上取一点D,DE∥AC,DF∥AB.(为说理方便,统一标注了数字表示的角).
∵DE∥AC(已知),
∴∠C=∠___,根据___;
又∵DE∥AC(已知),得∠2=∠4,根据___;
∵DF∥AB(已知),∴∠B=∠___,根据___;
又∵DF∥AB(已知),∴∠A=∠___,根据___;
∵∠A+∠B+∠C=∠___+∠___+___(根据上述求得等量代换)
又∠2=∠4,∴∠A+∠B+∠C=∠___+∠___+___=180°,根据___.
∵DE∥AC(已知),
∴∠C=∠___,根据___;
又∵DE∥AC(已知),得∠2=∠4,根据___;
∵DF∥AB(已知),∴∠B=∠___,根据___;
又∵DF∥AB(已知),∴∠A=∠___,根据___;
∵∠A+∠B+∠C=∠___+∠___+___(根据上述求得等量代换)
又∠2=∠4,∴∠A+∠B+∠C=∠___+∠___+___=180°,根据___.

▼优质解答
答案和解析
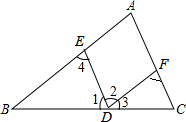 ∵DE∥AC(已知),
∵DE∥AC(已知),
∴∠C=∠1,根据两直线平行,同位角相等;
又∵DE∥AC(已知),得∠2=∠4,根据两直线平行,内错角相等;
∵DF∥AB(已知),∴∠B=∠3,根据两直线平行,同位角相等;
又∵DF∥AB(已知),∴∠A=∠DFC,根据两直线平行,同位角相等;
∵∠A+∠B+∠C=∠DFC+∠3+∠1(根据上述求得等量代换)
又∠2=∠4,∴∠A+∠B+∠C=∠2+∠3+∠1=180°,根据平角的定义.
故答案为:1,两直线平行,同位角相等,两直线平行,3,两直线平行,内错角相等,DFC,两直线平行,同位角相等,两直线平行,同位角相等,DFC,3,1,2,3,1,根据平角的定义.
 ∵DE∥AC(已知),
∵DE∥AC(已知),∴∠C=∠1,根据两直线平行,同位角相等;
又∵DE∥AC(已知),得∠2=∠4,根据两直线平行,内错角相等;
∵DF∥AB(已知),∴∠B=∠3,根据两直线平行,同位角相等;
又∵DF∥AB(已知),∴∠A=∠DFC,根据两直线平行,同位角相等;
∵∠A+∠B+∠C=∠DFC+∠3+∠1(根据上述求得等量代换)
又∠2=∠4,∴∠A+∠B+∠C=∠2+∠3+∠1=180°,根据平角的定义.
故答案为:1,两直线平行,同位角相等,两直线平行,3,两直线平行,内错角相等,DFC,两直线平行,同位角相等,两直线平行,同位角相等,DFC,3,1,2,3,1,根据平角的定义.
看了小学里我们已经学过三角形的三个...的网友还看了以下:
凭证应按日装订,凭证过多的可分若干册装订,凭证过少的可将同一月份若干日(不得超过7天)的凭证 2020-05-26 …
为什么通过醋酸和碳酸钠反应2CH3COOH+Na2CO3==2CH3COONa+H2O+CO2就能 2020-06-29 …
论证1+2=3迄今为止,听说都没有谁论证成功1+1=2,而其它则在1+1=2的基础上论证成功了…… 2020-07-02 …
论点:成功不是一蹴而就,需要一个漫长的过程成功不是一蹴而就,需要一个漫长的过程围绕这个论点用比喻论 2020-07-23 …
三角形内角和的求证方式很多,其中一种是通过顶点做平行辅助线,根据平行线内错角相等原理求证出三角形内 2020-08-01 …
观察下列各式及其验证过程:验证:=;验证:===;验证:=;验证:===.(1)按照上述两个等式及 2020-08-03 …
回答下列与水有关的问题:(1)在过滤、蒸馏二种操作中,能使硬水软化的是;(2)通过实验并验证其生成物 2020-11-05 …
验证过氧化氢酶催化过氧化氢高效性实验中,保证实验成功的最关键因素是()A.试管是否洁净B.肝脏是否新 2020-12-04 …
下列有关孟德尔的“假说-演绎法”的叙述中正确的是()A.通过“一对相对性状的遗传实验”证明了两大遗传 2020-12-14 …
如图,按规定,一块模板中AB,CD的延长线相交成85°的角,因交点不在板上,不便测量,如果你是技术工 2020-12-14 …