早教吧作业答案频道 -->数学-->
“城市呼唤绿化”,发展园林绿化事业是促进国家经济法阵和城市建设事业的重要组成部分,某城市响应城市绿化的号召,计划建一如图所示的三角形ABC形状的主题公园,其中一边利用现成
题目详情
“城市呼唤绿化”,发展园林绿化事业是促进国家经济法阵和城市建设事业的重要组成部分,某城市响应城市绿化的号召,计划建一如图所示的三角形ABC形状的主题公园,其中一边利用现成的围墙BC,长度为100
米,另外两边AB,AC使用某种新型材料围成,已知∠BAC=120°,AB=x,AC=y(x,y单位均为米).
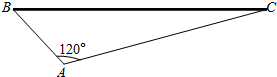
(1)求x,y满足的关系式(指出x,y的取值范围);
(2)在保证围成的是三角形公园的情况下,如何设计能使所用的新型材料总长度最短?最短长度是多少?
| 3 |

(1)求x,y满足的关系式(指出x,y的取值范围);
(2)在保证围成的是三角形公园的情况下,如何设计能使所用的新型材料总长度最短?最短长度是多少?
▼优质解答
答案和解析
(1)在△ABC中,由余弦定理,得AB2+AC2-2AB•ACcosA=BC2,
所以x2+y2-2xycos120°=30000,
即x2+y2+xy=30000,…(4分)
又因为x>0,y>0,所以0<x<100
,0<y<100
.…(6分)
(2)要使所用的新型材料总长度最短只需x+y的最小,
由(1)知,x2+y2+xy=30000,所以(x+y)2-30000=xy,
因为xy≤(
)2,所以(x+y)2-30000≤(
)2,…(9分)
则(x+y)2≤40000,即x+y≤200,
当且仅当x=y=100时,上式不等式成立.…(11分)
故当AB,AC边长均为100米时,所用材料长度最短为200米.…(12分)
所以x2+y2-2xycos120°=30000,
即x2+y2+xy=30000,…(4分)
又因为x>0,y>0,所以0<x<100
| 3 |
| 3 |
(2)要使所用的新型材料总长度最短只需x+y的最小,
由(1)知,x2+y2+xy=30000,所以(x+y)2-30000=xy,
因为xy≤(
| x+y |
| 2 |
| x+y |
| 2 |
则(x+y)2≤40000,即x+y≤200,
当且仅当x=y=100时,上式不等式成立.…(11分)
故当AB,AC边长均为100米时,所用材料长度最短为200米.…(12分)
看了“城市呼唤绿化”,发展园林绿化...的网友还看了以下:
我国西部部分地区实行“生态移民”,其主要目的是()A.促进居民就业B.促进民族交流C.缓解人口对生 2020-05-17 …
教育对生产力的促进作用主要是通过( )来实现的。 A.教育促进社会变革B.教育促进科 2020-05-17 …
A、B两家百货商店促销相同的衬衣和袜子,衬衣和袜子的原价是:衬衣50元/件,5元/双.A店的促销方 2020-05-21 …
如图,若已知角1+角2=90度,角2+角3=90度若已知角1+角2=90度,角2+角3=90度,问 2020-06-06 …
读下图漫画《拔》。从实现科学发展的角度看,漫画寓意要求()A.坚持第一要务,促进经济发展B.把握核 2020-06-17 …
区分.肾上腺素.促肾上腺素.促肾上腺素释放激素.这三个分不清老师说促肾上腺素释放激素的促是名词.促 2020-06-20 …
2013年9月27日,国务院印发的《中国(上海)自由贸易试验区总体方案》提出,要坚持先行先试,以开 2020-06-20 …
菜农在塑料大棚内种植反季节蔬菜,有时人为地提高大棚中二氧化碳浓度,其主要目的是()A、使害虫窒息死 2020-06-29 …
下列有关促胰液素的叙述不正确的是()A.促胰液素是人们发现的第一种激素B.促胰液素能够强烈的促进消 2020-06-30 …
从文明发展的角度看,下图变化的积极意义主要在于促使中国古代政治()A.从血缘政治向官僚政治转变B. 2020-07-13 …