早教吧作业答案频道 -->数学-->
在平面直角坐标系中,点A、B分别在x轴、y轴上,点A与点C关于y轴对称,点E是线段AC上的点(点E不与点A、C重合)(1)若点A的坐标为(a,0),则点C的坐标为;(2)如图1,点F是线段AB上
题目详情
在平面直角坐标系中,点A、B分别在x轴、y轴上,点A与点C关于y轴对称,点E是线段AC上的点(点E不与点A、C重合)
(1)若点A的坐标为(a,0),则点C的坐标为___;
(2)如图1,点F是线段AB上的点,若∠BEF=∠BAO,∠BAO=2∠OBE,求证:AF=CE;
(3)如图2,若点D为AC上一点,连接ED,满足BE=BD,试探究∠ABE与∠DEC的关系.
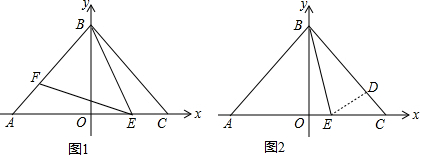
(1)若点A的坐标为(a,0),则点C的坐标为___;
(2)如图1,点F是线段AB上的点,若∠BEF=∠BAO,∠BAO=2∠OBE,求证:AF=CE;
(3)如图2,若点D为AC上一点,连接ED,满足BE=BD,试探究∠ABE与∠DEC的关系.

▼优质解答
答案和解析
(1)∵点A(a,0)与点C关于y轴对称,
∴C(-a,0),
故答案为(-a,0).,
(2)设∠OBE=α,
∴∠BAO=2∠OBE=2α,∠BEF=∠BAO=α,
由对称得,OA=OC,
∵BO⊥AC,
∴AB=CB,
∴∠BAO=∠BCO=2α,
∴∠ABE=∠ABO+∠OBE=90°-α,
在△BEF中,∠BFE=180°-(∠BEF+∠EBF)=90°-α,
∴∠ABE=∠BFE,
∴BE=EF,
在Rt△AOB中,∠ABO=90°-2α,
∴∠ACB=2α,∠CBO=∠90°-2α,
∵∠OBE=α,
∴∠CBE=90°-3α,
在△BCE中,根据三角形的内角和得,∠BEC=90°+α,
∴∠AEF=180°-∠BEF-∠BEC=90°-3α,
∴∠CBE=∠AEF,
在△AEF和△CBE中,
,
∴△AEF≌△CBE,
∴AF=CE,
(3)设∠OBE=α,∠CBE=β,
∴∠CBO=α+β,由(1)知,∠ABO=∠CBO=α+β,
∴∠ABE=∠ABO+∠OBE=α+β+α=2α+β,
在Rt△OBE中,∠OEB=90°-α,
在△BDE中,BD=BE,
∴∠BED=90°-
β,
∴∠DEC=180°-∠OEB-∠BED=
(2α+β),
∵∠ABE=2α+β,
∴∠ABE=2∠DEC.
∴C(-a,0),
故答案为(-a,0).,
(2)设∠OBE=α,
∴∠BAO=2∠OBE=2α,∠BEF=∠BAO=α,
由对称得,OA=OC,
∵BO⊥AC,
∴AB=CB,
∴∠BAO=∠BCO=2α,
∴∠ABE=∠ABO+∠OBE=90°-α,
在△BEF中,∠BFE=180°-(∠BEF+∠EBF)=90°-α,
∴∠ABE=∠BFE,
∴BE=EF,
在Rt△AOB中,∠ABO=90°-2α,
∴∠ACB=2α,∠CBO=∠90°-2α,
∵∠OBE=α,
∴∠CBE=90°-3α,
在△BCE中,根据三角形的内角和得,∠BEC=90°+α,
∴∠AEF=180°-∠BEF-∠BEC=90°-3α,
∴∠CBE=∠AEF,
在△AEF和△CBE中,
|
∴△AEF≌△CBE,
∴AF=CE,
(3)设∠OBE=α,∠CBE=β,
∴∠CBO=α+β,由(1)知,∠ABO=∠CBO=α+β,
∴∠ABE=∠ABO+∠OBE=α+β+α=2α+β,
在Rt△OBE中,∠OEB=90°-α,
在△BDE中,BD=BE,
∴∠BED=90°-
| 1 |
| 2 |
∴∠DEC=180°-∠OEB-∠BED=
| 1 |
| 2 |
∵∠ABE=2α+β,
∴∠ABE=2∠DEC.
看了在平面直角坐标系中,点A、B分...的网友还看了以下:
填空.线就要,三克油.(1)将一个圆柱的侧面展开是一个长18.84厘米,宽10厘米的长方形,这个圆 2020-04-27 …
列一个分式方程一个分数,如果分母加1,则分数的值变为十一分之一;如果分子加1,则分数的值就变为七分 2020-06-03 …
数学题之165一个最简分数,如果分子加上1,则分子比分母少1,如果分母加上1,则分数值是4分之3, 2020-07-18 …
1.某纸盒厂有工人49名,生产带盖纸盒.每个工人每小时生产12个盒身或者18个盒盖.一个合身陪两个 2020-07-19 …
一最简分数,如果分子加上1,分子则比分母少2;如果分母加上1,则分数值等于1/2,可以不用方程解么 2020-07-30 …
1.当k取何值时,100x^2-kxy+49y^2是一个完全平方数?2.2^48-1可以被60和70 2020-11-03 …
一个分数如果分子加1,则分数值为1,如果分母加1,则分数值为9分之8,这个原来是几 2020-11-06 …
判断下列命题的真假,并给出证明.(1}相等的角是对顶角;(2)若x≠1,则分式2x/x^2-1有意义 2020-12-13 …
填空1.一个数由15个百,15个十分之一,15个千分之一组成,这个数是.有个0.0012.有一个最简 2020-12-17 …
题目要求如下:一个分数的分子加上1,则分数值为1如果分母加一,则分数值为九分之八这个分数原来是多少? 2021-01-02 …