如图，将透明三角形纸片PAB的直角顶点P落在第四象限，顶点A、B分别落在反比例函数y=kx图象的两支上，且PB⊥x于点C，PA⊥y于点D，AB分别与x轴，y轴相交于点E、F．已知B（1

Question

如图，将透明三角形纸片PAB的直角顶点P落在第四象限，顶点A、B分别落在反比例函数y= (k)/(x)图象的两支上，且PB⊥x于点C，PA⊥y于点D，AB分别与x轴，y轴相交于点E、F．已知B（1，3）．

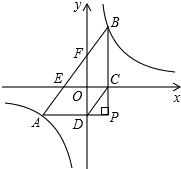
（1）k=___；
（2）试说明AE=BF；
（3）当四边形ABCD的面积为 (21)/(4)时，求点P的坐标．

Answer 1

（1）把B（1，3）代入y=(k)/(x)得k=1×3=3；
故答案为：3；

（2）反比例函数解析式为y=(3)/(x)，
设A点坐标为（a，(3)/(a)），
∵PB⊥x于点C，PA⊥y于点D，
∴D点坐标为（0，(3)/(a)），P点坐标为（1，(3)/(a)），C点坐标为（1，0），
∴PB=3-(3)/(a)，PC=-(3)/(a)，PA=1-a，PD=1，
∴(PC)/(PB)=(-(3)/(a))/(3-(3)/(a))=(1)/(1-a)，(PD)/(PA)=(1)/(1-a)，
∴(PC)/(PB)=(PD)/(PA)，
而∠CPD=∠BPA，
∴△PCD∽△PBA，
∴∠PCD=∠PBA，
∴CD∥BA，
而BC∥DF，AD∥EC，
∴四边形BCDF、ADCE都是平行四边形，
∴BF=CD，AE=CD，
∴BF=AE，

（3）∵四边形ABCD的面积=S_△PAB-S_△PCD，
∴(1)/(2)•（3-(3)/(a)）•（1-a）-(1)/(2)•1•（-(3)/(a)）=(21)/(4)，
整理得a+(3)/(2)=0，解得a=-(3)/(2)，
∴P点坐标为（1，-2）．