早教吧作业答案频道 -->数学-->
某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲,y乙(单位:元),y甲,y乙与销售数量x(单位:件)的函数关系如图所示,请根据图象解决下列问题:(1)分别求出y甲,y乙与x
题目详情
某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲,y乙(单位:元),y甲,y乙与销售数量x(单位:件)的函数关系如图所示,请根据图象解决下列问题:
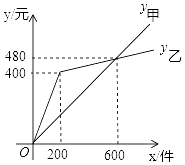
(1)分别求出y甲,y乙与x的函数关系式;
(2)现厂家分配该商品给甲、乙两商场共计1200件,当甲、乙商场售完这批商品,厂家可获得总利润的1080元,问厂家如何分配这批商品?

(1)分别求出y甲,y乙与x的函数关系式;
(2)现厂家分配该商品给甲、乙两商场共计1200件,当甲、乙商场售完这批商品,厂家可获得总利润的1080元,问厂家如何分配这批商品?
▼优质解答
答案和解析
(1)设y甲=kx(k≠0),y乙=mx+n,
将(600,480)代入y甲=kx,
480=600k,解得:k=0.8,
∴y甲与x的函数关系式为y甲=0.8x;
当0≤x≤200时,将(0,0)、(200,400)代入y乙=mx+n中,
,解得:
,
∴此时y乙=2x;
当200≤x时,将(200,400)、(600,480)代入y乙=mx+n中,
,解得:
,
∴此时y乙=0.2x+360.
∴y乙与x的函数关系式为y乙=
.
(2)设分配给乙商场x件,则分配给甲商场(1200-x)件,
当0≤x≤200时,有0.8×(1200-x)+2x=1080,
解得:x=100,
此时1200-x=1100;
当x≥200时,有0.8×(1200-x)+0.2x+360=1080,
解得:x=400,
此时1200-x=800.
答:厂家分配该商品给甲商场1100件乙商场100件或甲商场800件乙商场400件时,厂家可获得总利润的1080元.
将(600,480)代入y甲=kx,
480=600k,解得:k=0.8,
∴y甲与x的函数关系式为y甲=0.8x;
当0≤x≤200时,将(0,0)、(200,400)代入y乙=mx+n中,
|
|
∴此时y乙=2x;
当200≤x时,将(200,400)、(600,480)代入y乙=mx+n中,
|
|
∴此时y乙=0.2x+360.
∴y乙与x的函数关系式为y乙=
|
(2)设分配给乙商场x件,则分配给甲商场(1200-x)件,
当0≤x≤200时,有0.8×(1200-x)+2x=1080,
解得:x=100,
此时1200-x=1100;
当x≥200时,有0.8×(1200-x)+0.2x+360=1080,
解得:x=400,
此时1200-x=800.
答:厂家分配该商品给甲商场1100件乙商场100件或甲商场800件乙商场400件时,厂家可获得总利润的1080元.
看了某厂家在甲、乙两家商场销售同一...的网友还看了以下:
懂概率的来甲乙两位好友,甲去上某课时,乙去概率为0.9,甲不去上该课时,乙不去概率也为0.9,甲去 2020-05-23 …
我们常常把一类数学题型叫做“某某问题”,比如工程问题、行程问题、浓度配比问题等,请看,下面这类题型 2020-08-01 …
如图为某家系的遗传系谱图,其中乙病为伴X染色体隐性遗传病.甲病用A、a表示,乙病用B、b表示.请据图 2020-11-14 …
图1为某家系的遗传系谱,其中甲病(基因用A、a表示)、乙病(基因用B、b表示)是两种单基因遗传病,请 2020-11-14 …
(14分)如图为某家系的系谱图,甲病(A—a)与乙病(B—b)都是单基因遗传病,其中一种病为伴性遗传 2020-11-14 …
关于追诉期?甲某伙同乙某于2005年4月盗窃自行车10辆,案值2000元.2010年5月乙某再次盗窃 2020-11-30 …
(14分)如图为某家系的系谱图,甲病(A—a)与乙病(B—b)都是单基因遗传病,其中一种病为伴性遗传 2020-12-20 …
某家系中有甲、乙两种单基因遗传病(如图),其中一种是伴性遗传病,甲病(设基因为B、b)和乙病(设基因 2020-12-25 …
分析有关遗传病的资料,回答问题图1是某家系甲、乙两种单基因遗传病的系谱图,其基因分别用D、d和E、e 2020-12-25 …
图1是某家系甲、乙两种单基因遗传病系谱图,其基因分别用A、a和B、b表示,其中乙病为伴性遗传病;图2 2020-12-25 …