早教吧作业答案频道 -->数学-->
如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连结BD、CD.(1)判断BD与AC的位置关系和数量关系,并证明;(2)如图2,若将△DCE绕点E旋转一定的角度后,BD与AC的位置关系和
题目详情
如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连结BD、CD.
(1)判断BD与AC的位置关系和数量关系,并证明;
(2)如图2,若将△DCE绕点E旋转一定的角度后,BD与AC的位置关系和数量关系是否发生变化?并证明;
(3)如图3,将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,求BD与AC夹角的度数.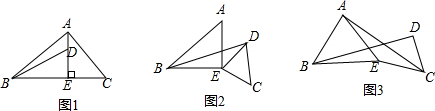
(1)判断BD与AC的位置关系和数量关系,并证明;
(2)如图2,若将△DCE绕点E旋转一定的角度后,BD与AC的位置关系和数量关系是否发生变化?并证明;
(3)如图3,将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,求BD与AC夹角的度数.

▼优质解答
答案和解析
(1)BD与AC的位置关系是:BD⊥AC,数量关系是BD=AC.
理由如下:
延长BD交AC于点F.
∵AE⊥BC于E,
∴∠BED=∠AEC=90°.
∵AE=BE,DE=CE,
∴△DBE≌△CAE,
∴BD=AC,∠DBE=∠CAE,∠BDE=∠ACE.
∵∠BDE=∠ADF,
∴∠ADF=∠ACE.
∵∠ACE+∠CAE=90°,
∴∠ADF+∠CAE=90°,
∴BD⊥AC.
(2)①∵∠AEB=∠DEC=90°,
∴∠AEB+∠AED=∠DEC+∠AED,
即∠BED=∠AEC.
∵AE=BE,DE=CE,
∴△BED≌△AEC,
∴BD=AC,∠BDE=∠ACE,∠DBE=∠CAE.
∵∠BFC=∠ACD+∠CDE+∠BDE=∠ACD+∠CDE+∠ACE=90°,
∴BD⊥AC.
②BD与AC的数量关系是:BD=AC.
∵△ABE和△DCE是等边三角形,
∴∠AEB=∠ABE=60°,AE=BE,
∠DEC=∠DCE=60°,DE=CE,
∴∠AEB+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
∴△BED≌△AEC.
∴BD=AC.
(3)∵△ABE和△DEC是等边三角形,
∴AE=BE,DE=EC,∠EDC=∠DCE=60°,∠BEA=∠DEC=60°,
∴∠BEA+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
在△BED和△AEC中,
∴△BED≌△AEC,
∴∠BED=∠ACE,
∴∠DFC=180°-(∠BDE+∠EDC+∠DCF)=60°
∴BD与AC的夹角度数为60°或120°.
理由如下:
延长BD交AC于点F.
∵AE⊥BC于E,
∴∠BED=∠AEC=90°.
∵AE=BE,DE=CE,
∴△DBE≌△CAE,
∴BD=AC,∠DBE=∠CAE,∠BDE=∠ACE.
∵∠BDE=∠ADF,
∴∠ADF=∠ACE.
∵∠ACE+∠CAE=90°,
∴∠ADF+∠CAE=90°,
∴BD⊥AC.
(2)①∵∠AEB=∠DEC=90°,
∴∠AEB+∠AED=∠DEC+∠AED,
即∠BED=∠AEC.
∵AE=BE,DE=CE,
∴△BED≌△AEC,
∴BD=AC,∠BDE=∠ACE,∠DBE=∠CAE.
∵∠BFC=∠ACD+∠CDE+∠BDE=∠ACD+∠CDE+∠ACE=90°,
∴BD⊥AC.
②BD与AC的数量关系是:BD=AC.
∵△ABE和△DCE是等边三角形,
∴∠AEB=∠ABE=60°,AE=BE,
∠DEC=∠DCE=60°,DE=CE,
∴∠AEB+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
∴△BED≌△AEC.
∴BD=AC.
(3)∵△ABE和△DEC是等边三角形,
∴AE=BE,DE=EC,∠EDC=∠DCE=60°,∠BEA=∠DEC=60°,
∴∠BEA+∠AED=∠DEC+∠AED,
∴∠BED=∠AEC,
在△BED和△AEC中,
|
∴△BED≌△AEC,
∴∠BED=∠ACE,
∴∠DFC=180°-(∠BDE+∠EDC+∠DCF)=60°
∴BD与AC的夹角度数为60°或120°.
看了如图1,在△ABC中,AE⊥B...的网友还看了以下:
取一副三角板按图1拼接,固定三角板ADC,将三角板ABC绕点A按顺时针方向旋转一个大小为α的角(0 2020-05-01 …
把图中的五角星图案,绕着它的中心点O旋转,旋转角为多少度,旋转后的五角星能与自身重合?对等%把图中 2020-05-16 …
将一个直角三角形饶他的斜边旋转一周是什么图形,谁帮我画个出来谢了画一个直角三角形绕斜边旋转一周的图 2020-06-19 …
如图1,一副三角板的两个直角重叠在一起,∠A=30°,∠C=45°△COD固定不动,△AOB绕着O 2020-06-20 …
将一副三角板如图1摆放.∠AOB=60°,∠COD=45°,OM平分AOD,ON平分∠COB.(1 2020-07-14 …
如图1、图2,△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90°,(1)在图1中,A 2020-07-26 …
在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动 2020-08-01 …
如图1,△ABC为等边三角形,△ADE是△ABC的位似图形,位似比为k:1,点D在AB上,点E在A 2020-08-02 …
数字图像处理图像绕点旋转几何变换怎么求1.设灰度级为8的子图像f(x,y)=[01267;12345 2020-10-31 …
将一副三角板按如图1的位置摆放.(1)∠1与∠2的关系为.(2)在图1中,若EM平分∠BED,EN平 2020-11-13 …