早教吧作业答案频道 -->数学-->
如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.求证:△AGE≌△AFE;(2)如图3,连接BD交AE
题目详情
如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
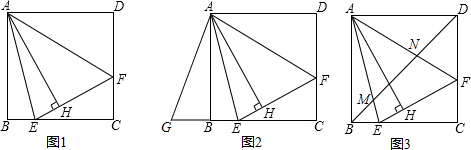
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.求证:△AGE≌△AFE;
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.

(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.求证:△AGE≌△AFE;
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
▼优质解答
答案和解析
(1)由旋转的性质可知:AF=AG,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中
,
∴△GAE≌△FAE(SAS);
(2)如图所示:将△ABM逆时针旋转90°得△ADM′.
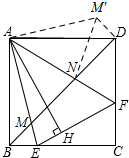
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°.
由旋转的性质可知:∠ABM=∠ADM′=45°,BE=DM′.
∴∠NDM′=90°.
∴NM′2=ND2+DM′2.
∵∠EAM′=90°,∠EAF=45°,
∴∠EAF=∠FAM′=45°.
在△AMN和△ANM′中,
,
∴△AMN≌△ANM′(SAS).
∴MN=NM′.
又∵BM=DM′,
∴MN2=ND2+BM2.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中
|
∴△GAE≌△FAE(SAS);
(2)如图所示:将△ABM逆时针旋转90°得△ADM′.

∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°.
由旋转的性质可知:∠ABM=∠ADM′=45°,BE=DM′.
∴∠NDM′=90°.
∴NM′2=ND2+DM′2.
∵∠EAM′=90°,∠EAF=45°,
∴∠EAF=∠FAM′=45°.
在△AMN和△ANM′中,
|
∴△AMN≌△ANM′(SAS).
∴MN=NM′.
又∵BM=DM′,
∴MN2=ND2+BM2.
看了如图1,在正方形ABCD内作∠...的网友还看了以下:
在平面直角坐标系中,对于平面内任何一点(a,b),若规定以下三种变换:①f(a,b)=(-a,b) 2020-04-26 …
在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:1f(a,b)=(-a,b). 2020-04-26 …
Matlab求帮忙看看哪里错了.h=0;%h[0,51.5]a=15;m=sMatlab求帮忙看看 2020-05-13 …
读下面的流程图,其最后结果是(3)。A.将X,Y,Z按从大到小的顺序排序B.将X,Y,Z按从小到大的 2020-05-26 …
这3个土方开挖公式分别适用在什么情况下的?刚开始做结算,V=(a+2c+kh)*(b+2c+kh) 2020-06-10 …
三角形角边长为3和9,第三边的高为h的取值范围是()A.0<h<3B.0<h≤3C.3<h<9D. 2020-06-10 …
如图所示,A物体用板托着,位于离地h=1.6m处,轻质细绳通过光滑定滑轮与A、B相连,绳子处于绷直 2020-06-29 …
如图水银柱上面封闭一段气体,管内外水银面高度差h=72cm,大气压强为76cmHg,正确的是()A. 2020-11-11 …
导数的几何意义练习题1.曲线y=-2x2+1在点(0,1)处的切线的斜率是多少?2.曲线y=1/2x 2021-01-22 …
3.y=a(x-h+p)+k4.y=a(x-h-f)+k又没有详解?y=a(x-h)+k移动后的解析 2021-02-05 …