早教吧作业答案频道 -->数学-->
在矩形ABCD中,AB=4,BC=8,经过对角线交点O的直线EF绕点O旋转,分别交AD、BC于点E、F,连接AF、CE.(1)如图(1),依据下列条件在普通四边形、梯形、普通平行四边形、矩菱形或正方形中选
题目详情
在矩形ABCD中,AB=4,BC=8,经过对角线交点O的直线EF绕点O旋转,分别交AD、BC于点E、F,连接AF、CE.
(1)如图(1),依据下列条件在普通四边形、梯形、普通平行四边形、矩菱形或正方形中选择填空:旋转过程中四边形AFCE始终为___;
当点E为AD的中点时四边形AFCE为___;
当EF⊥AC时四边形AFCE为___;
(2)如图(1),当EF⊥AC时,求AF的长;
(3)如图(2),在(2)的基础上,若动点P从A点出发,沿A→F→B→A运动一周停止,速度为每秒5厘米;同时点Q从C点出发,沿C→D→E→C运动一周停止,速度为每秒4厘米,在P、Q运动过程中,第几秒时,四边形APCQ是平行四边形?
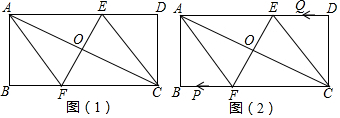
(1)如图(1),依据下列条件在普通四边形、梯形、普通平行四边形、矩菱形或正方形中选择填空:旋转过程中四边形AFCE始终为___;
当点E为AD的中点时四边形AFCE为___;
当EF⊥AC时四边形AFCE为___;
(2)如图(1),当EF⊥AC时,求AF的长;
(3)如图(2),在(2)的基础上,若动点P从A点出发,沿A→F→B→A运动一周停止,速度为每秒5厘米;同时点Q从C点出发,沿C→D→E→C运动一周停止,速度为每秒4厘米,在P、Q运动过程中,第几秒时,四边形APCQ是平行四边形?

▼优质解答
答案和解析
(1)当点E为AD的中点时,四边形AFCE为平行四边形;理由如下:
∵四边形ABCD是矩形,
∴AD∥BC,OA=OC,
∴∠CAD=∠ACB,∠AEF=∠CFE.
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴AE=CF.
又∵AE∥CF,
∴四边形AFCE为平行四边形;
当点E为AD的中点时,AE=CF,AE∥CF,
则四边形AFCE为平行四边形;
当EF⊥AC时,四边形AFCE为菱形,理由如下:
∵由①知四边形AFCE为平行四边形,
∵EF⊥AC,
∴四边形AFCE为菱形;
故答案为:平行四边形;平行四边形;菱形.
(2) 设菱形的边长AF=CF=xcm,则BF=(8-x)cm,
在Rt△ABF中,AB=4cm,
由勾股定理得:AB2+BF2=AF2,
即42+(8-x)2=x2,
解得:x=5,
∴AF=5;
(3) 根据题意得,P点AF上时,Q点CD上,此时A,C,P,Q四点不可能构成平行四边形;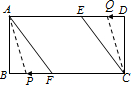
同理P点AB上时,Q点DE或CE上,也不能构成平行四边形.
∴只有当P点在BF上,Q点在ED上时,才能构成平行四边形,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,
PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12-4t,
∴5t=12-4t,
解得:t=
,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,t=
秒.
∵四边形ABCD是矩形,
∴AD∥BC,OA=OC,
∴∠CAD=∠ACB,∠AEF=∠CFE.
在△AOE和△COF中,
|
∴△AOE≌△COF(AAS),
∴AE=CF.
又∵AE∥CF,
∴四边形AFCE为平行四边形;
当点E为AD的中点时,AE=CF,AE∥CF,
则四边形AFCE为平行四边形;
当EF⊥AC时,四边形AFCE为菱形,理由如下:
∵由①知四边形AFCE为平行四边形,
∵EF⊥AC,
∴四边形AFCE为菱形;
故答案为:平行四边形;平行四边形;菱形.
(2) 设菱形的边长AF=CF=xcm,则BF=(8-x)cm,
在Rt△ABF中,AB=4cm,
由勾股定理得:AB2+BF2=AF2,
即42+(8-x)2=x2,
解得:x=5,
∴AF=5;
(3) 根据题意得,P点AF上时,Q点CD上,此时A,C,P,Q四点不可能构成平行四边形;

同理P点AB上时,Q点DE或CE上,也不能构成平行四边形.
∴只有当P点在BF上,Q点在ED上时,才能构成平行四边形,
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,
PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12-4t,
∴5t=12-4t,
解得:t=
| 4 |
| 3 |
∴以A,C,P,Q四点为顶点的四边形是平行四边形时,t=
| 4 |
| 3 |
看了在矩形ABCD中,AB=4,B...的网友还看了以下:
我们把上端开口、下端连通的容器叫做连通器.连通器有个特点,即在液体不流动的情况下,各容器中的液面都 2020-04-07 …
关于连通器,下列说法正确的是()A.微小压强计是利用连通器的原理研究液体压强的B.连通器中只要液体 2020-05-13 …
状态检测是一种高级通信过滤,他检测传输层协议信息并且监控基于连接的应用层协议状态,对于所有连接,每个 2020-05-31 …
得了咽喉炎会引发中耳炎的原因是[]A.细菌、病毒连通于咽和鼓室之间B.咽鼓管连通于咽和鼓室之间C. 2020-06-23 …
连通器是我们日常生活中很常见的一种容器,下列关于连通器的说法不正确的是()A.上端封口、下端连通的 2020-06-30 …
如图所示,两个半圆形的光滑细管道(管道内径远小于半圆形半径)在竖直平面内交叠,组成“S”字形通道. 2020-07-31 …
关于连通器的理解正确的()A.连通器中至少有两个开口B.连通器中只有两个开口C.在连通器中倒入液体后 2020-11-04 …
连通器是我们日常生活中很常见的一种容器,下列关于连通器的说法不正确的是()A.上端封口、下端连通的容 2020-11-04 …
(bddd•连云港)如7是一回形7,其回形通道的宽和OB的长均为0,回形线与射线OA交于A0,Ab, 2020-11-12 …
有向图的强连通图或者是无向图的连通图是不是都是回路呢?还有关于连通分量和强连通分量是如何解出来的? 2020-12-27 …