早教吧作业答案频道 -->数学-->
问题背景如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.类比探究如图2,在正△ABC的内部,作∠
题目详情
问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
类比探究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)
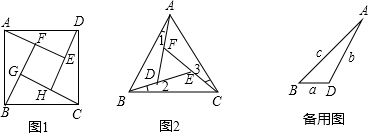
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.
(2)△DEF是否为正三角形?请说明理由.
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
类比探究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)

(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.
(2)△DEF是否为正三角形?请说明理由.
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.
▼优质解答
答案和解析
(1)△ABD≌△BCE≌△CAF;理由如下:
∵△ABC是正三角形,
∴∠CAB=∠ABC=∠BCA=60°,AB=BC,
∵∠ABD=∠ABC-∠2,∠BCE=∠ACB-∠3,∠2=∠3,
∴∠ABD=∠BCE,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(ASA);
(2)△DEF是正三角形;理由如下:
∵△ABD≌△BCE≌△CAF,
∴∠ADB=∠BEC=∠CFA,
∴∠FDE=∠DEF=∠EFD,
∴△DEF是正三角形;
(3)作AG⊥BD于G,如图所示:
∵△DEF是正三角形,
∴∠ADG=60°,
在Rt△ADG中,DG=
b,AG=
b,
在Rt△ABG中,c2=(a+
b)2+(
b)2,
∴c2=a2+ab+b2.
∵△ABC是正三角形,
∴∠CAB=∠ABC=∠BCA=60°,AB=BC,
∵∠ABD=∠ABC-∠2,∠BCE=∠ACB-∠3,∠2=∠3,
∴∠ABD=∠BCE,
在△ABD和△BCE中,
|
∴△ABD≌△BCE(ASA);
(2)△DEF是正三角形;理由如下:
∵△ABD≌△BCE≌△CAF,

∴∠ADB=∠BEC=∠CFA,
∴∠FDE=∠DEF=∠EFD,
∴△DEF是正三角形;
(3)作AG⊥BD于G,如图所示:
∵△DEF是正三角形,
∴∠ADG=60°,
在Rt△ADG中,DG=
| 1 |
| 2 |
| ||
| 2 |
在Rt△ABG中,c2=(a+
| 1 |
| 2 |
| ||
| 2 |
∴c2=a2+ab+b2.
看了问题背景如图1,在正方形ABC...的网友还看了以下:
为什么总感觉自己背诵英语单词的效率很低1.我老是背了.然后半小时后就忘了.2.背完了,去做题发现一 2020-05-13 …
关于中学课文《背影》的几个问题!急~!1.在《背影》中,描写背影的那段文字中,作者着力刻画了父亲怎 2020-05-17 …
背对背布置的机柜或机架背面之间的距离不应小于( )米。A.1 B.2.6C.1.5 D.1.2 2020-05-26 …
如图,沿水库拦水坝面的背水坡八面加宽2米,坡度由原来的1比2变成1比2.5.已知原背水坡长bd等于 2020-06-24 …
给有括号的字选择正确的解释1.为(难)()1做起来费事2使感到困难3不容易4不好2.(负)荆请罪( 2020-07-11 …
怎么学好英语英语还是零基础.打算开始拼搏一下,想努力搞好英语,就是遇到几个疑问1.我不知道怎么学, 2020-07-25 …
如图,某一大坝的横截面是梯形ABCD,坝顶宽CD=3m,坝高6m,迎水坡BC的坡度i=1:2,背水坡 2020-11-08 …
从左到右放有60张卡片,小饶按从左到右的顺序在卡片上依次写上1,2,1,2,1,2,1,2,1,…; 2020-11-10 …
背英语单词的几个问题1一天背多少个?2一天背单词时间不少于多长?3背课本上的还是背小字典上的?4怎样 2021-02-05 …
英语记单词方法英语及格线附近徘徊,想把英语提上去从网上看了不少背单词的方法,有几个问题想问1.背单词 2021-02-05 …