早教吧作业答案频道 -->数学-->
已知,点D为直线BC上一动点(点D不与点B、C重合),∠BAC=90°,AB=AC,∠DAE=90°,AD=AE,连接CE.(l)如图1,当点D在线段BC上时,求证:①BD⊥CE,②CE=BC-CD;(2)如图2,当点D在线段BC的延长
题目详情
已知,点D为直线BC上一动点(点D不与点B、C重合),∠BAC=90°,AB=AC,∠DAE=90°,AD=AE,连接CE.
(l)如图1,当点D在线段BC上时,求证:①BD⊥CE,②CE=BC-CD;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CE、BC、CD三条线段之间的关系;
(3)如图3,当点O在线段BC的反向延长线上时,且点A、E分别在直线BC的两侧,点F是DE的中点,连接AF、CF,其他条件不变,请判断△ACF的形状,并说明理由.
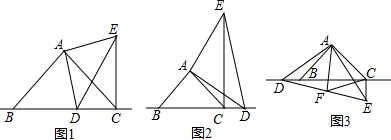
(l)如图1,当点D在线段BC上时,求证:①BD⊥CE,②CE=BC-CD;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CE、BC、CD三条线段之间的关系;
(3)如图3,当点O在线段BC的反向延长线上时,且点A、E分别在直线BC的两侧,点F是DE的中点,连接AF、CF,其他条件不变,请判断△ACF的形状,并说明理由.

▼优质解答
答案和解析
(1)证明:如图1中,∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,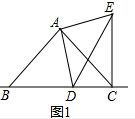
,
∴△ABD≌△ACE,
∴∠ABD=∠ACE=45°,BD=CE,
∴∠ACB+∠ACE=90°
∴∠ECB=90°,
∴BD⊥CE,CE=BC-CD.
(2)如图2中,结论:CE=BC+CD,理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,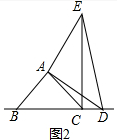
,
∴△ABD≌△ACE,
∴BD=CE,
∴CE=BC+CD.
(3)如图3中,结论:△ACF是等腰三角形.理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
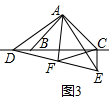
∴△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠ABC=∠ACB=45°,
∴∠ACE=∠ABD=135°,
∴∠DCE=90°,
又∵点F是DE中点,
∴AF=CF=
DE,
∴△ACF是等腰三角形.
∴∠BAD=∠CAE,
在△ABD和△ACE中,

|
∴△ABD≌△ACE,
∴∠ABD=∠ACE=45°,BD=CE,
∴∠ACB+∠ACE=90°
∴∠ECB=90°,
∴BD⊥CE,CE=BC-CD.
(2)如图2中,结论:CE=BC+CD,理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,

|
∴△ABD≌△ACE,
∴BD=CE,
∴CE=BC+CD.
(3)如图3中,结论:△ACF是等腰三角形.理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
|

∴△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠ABC=∠ACB=45°,
∴∠ACE=∠ABD=135°,
∴∠DCE=90°,
又∵点F是DE中点,
∴AF=CF=
| 1 |
| 2 |
∴△ACF是等腰三角形.
看了已知,点D为直线BC上一动点(...的网友还看了以下:
1、正值壮年,应知不朽方为寿;恰当而立,须知文章可永龄.2、不活正当同心创业;无虞奋发共1、正值壮年 2020-03-30 …
解不等式|3x-2|-|x-6|>1(1)、当x≥6时3x+2-x+6>12x>-7所以解是x≥6 2020-04-26 …
1.当-2≤x≥2时,求函数y=x²-2x-3的取值范围2.当x≥0时,求函数y=-x(2-x)的 2020-05-16 …
(2)“锐不可当”的问题?1).“锐不可当”和“锐不可挡”都是词语吗?2).“锐不可当”的“当”的 2020-06-26 …
“锐不可当”的问题?请问:锐不可当的“当”是第一声还是第四声呢.我想问的问题还有:1)。“锐不可当 2020-06-26 …
函数f(X)=[X]的函数值表示不超过X的最大整数疑惑!函数f(x)=[x]的函数值表示不超过x的 2020-06-27 …
解不等式|x-2|≤1时,我们可以采用下面的解法:①.当x-2≥0时,|x-2|=x-2∴原不等式 2020-07-03 …
科学问题有一支刻度不正确(但刻度均匀)的温度计1,把他与一直标准的温度计2对比后发现,当2的温度为 2020-07-13 …
整式mx+2n的值随x的取值不同而不同,下表是当x取不同值时对应的整式的值,则关于x的方程-mx- 2020-08-02 …
已知数列{An}满足A1=a,A(n+1)=1+1/An,我们知道当a取不同的值时高考数列问题求解 2020-08-02 …