某次摩托车的特技表演可简化为如下模型，AB是长度为x的水平顶，BC是半径为2R的14圆弧，DEG是半径为R的34圆弧，D点在C点正上方，G点距右侧水平面高度为R，质量为m的摩托车（可视为质点）

Question

某次摩托车的特技表演可简化为如下模型，AB是长度为x的水平顶，BC是半径为2R的(1)/(4)圆弧，DEG是半径为R的(3)/(4)圆弧，D点在C点正上方，G点距右侧水平面高度为R，质量为m的摩托车（可视为质点）在大小恒定的牵引力F作用下从A点由静止出发，牵引力在ABC段的大小恒为F，摩托车经过C点时关闭发动机，之后沿竖直方向从D点进入上面的轨道做圆周运动，从G点脱离上方轨道，进入右侧水平面，已知重力加速度为g，假设在ABC段摩托车所受阻力恒定，且为重力的k倍，忽略其在DEG段及空气中所受的阻力

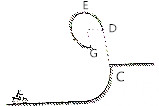
（1）为了使摩托车能安全通过轨道，求力F的最小值；
（2）若摩托车离开C点速度大小是√(10gR)，判断摩托车能否安全通过上方圆弧轨道，若不能通过，计算在C点时应具有的最小速度；若能通过，求摩托车落在右侧水平面的位置距离C点多远．

Answer 1

（1）为了使摩托车安全通过轨道，在E点有最小速度，根据mg=m(vE2)/(R)，
解得vE=√(gR)，
对A到E的过程运用动能定理得，F（x+πR）-kmg（x+πR）-mg（2R+R+2R）=(1)/(2)mvE2-0，
解得最小F=(5.5mgR+kmg(x+πR))/(x+πR)．
（2）对C到E运用动能定理得，-mg•3R=(1)/(2)mvE′2-(1)/(2)mvc2，
解得v_E′=√(4gR)>v_E，知摩托车能安全通过上方的圆弧轨道，
对C到G点运用动能定理得，-mgR=(1)/(2)mvG2-(1)/(2)mvC2，
解得v_G=√(8gR)，
根据R=(1)/(2)gt2得，t=√((2R)/(g))，
则摩托车落在右侧水平面的位置距离C点的距离x=v_Gt-R=4R-R=3R．
答：（1）力F的最小值为(5.5mgR+kmg(x+πR))/(x+πR)．
（2）能安全通过上方圆弧轨道，摩托车落在右侧水平面的位置距离C点3R．