早教吧作业答案频道 -->数学-->
如图,把一块含45°直角三角板的锐角顶点与正方形ABCD的顶点A重合.正方形ABCD固定不动,让三角板绕点A旋转.(1)当三角板绕点A旋转到如图①的位置时,含45°角的两边分别与正方形
题目详情
如图,把一块含45°直角三角板的锐角顶点与正方形ABCD的顶点A重合.正方形ABCD固定不动,让三角板绕点A旋转.
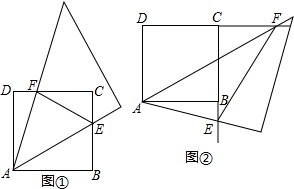
(1)当三角板绕点A旋转到如图①的位置时,含45°角的两边分别与正方形的边BC、DC交于点E、F,求证:EF=BE+DF;
(2)当三角板绕点A旋转到如图②的位置时,含45°角的两边分别与正方形的CB、DC两边的延长线交于点E、F.试写出EF、BE和DF三条线段满足的数量关系,不必证明.
(3)在图①中,当正方形ABCD的边长为6,EF=5,BE的长为___.

(1)当三角板绕点A旋转到如图①的位置时,含45°角的两边分别与正方形的边BC、DC交于点E、F,求证:EF=BE+DF;
(2)当三角板绕点A旋转到如图②的位置时,含45°角的两边分别与正方形的CB、DC两边的延长线交于点E、F.试写出EF、BE和DF三条线段满足的数量关系,不必证明.
(3)在图①中,当正方形ABCD的边长为6,EF=5,BE的长为___.
▼优质解答
答案和解析
(1)EF=BE+DF.
延长FD至G,使DG=BE,连接AG,如图①,
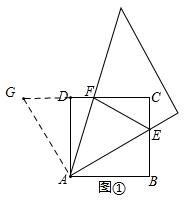
∵ABCD是正方形,
∴AB=AD,∠ABE=ADG=∠DAB=90°,
∴△ABE≌△ADG,
∴AE=AG,∠DAG=∠EAB,
∵∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠DAF+∠DAG=45°,
∴∠GAF=∠EAF=45°,
∵AF=AF,
∴△GAF≌△EAF,
∴EF=GF,
∴GF=DF+DG=DF+BE,
即:EF=DF+BE.
(2)EF=DF-BE.
在DC上截取DH=BE,连接AH,如图②,
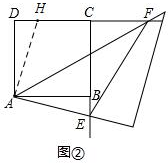
∵AD=AB,∠ADH=∠ABE=90°,
∴△ADH≌△ABE(SAS),
∴AH=AE,∠DAH=∠EAB,
∵∠EAF=∠EAB+∠BAF=45°,
∴∠DAH+∠BAF=45°,
∴∠HAF=45°=∠EAF,
∵AF=AF,
∴△HAF≌EAF(SAS),
∴HF=EF,
∵DF=DH+HF,
∴EF=DF-BE.
(3)如图③,
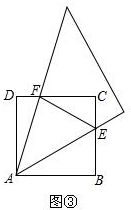
由(1)中结论可知:EF=DF+BE,
∵AB=BC=CD=AD=6,
设BE=x,则CE=6-x,
∵EF=5,
∴DF=5-x,
∴FC=1+x,
在Rt△CEF中,EF2=FC2+CE2,
∴25=(1+x)2+(6-x)2,
解得:x=2或x=3,
即BE的长为2或3.
延长FD至G,使DG=BE,连接AG,如图①,

∵ABCD是正方形,
∴AB=AD,∠ABE=ADG=∠DAB=90°,
∴△ABE≌△ADG,
∴AE=AG,∠DAG=∠EAB,
∵∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠DAF+∠DAG=45°,
∴∠GAF=∠EAF=45°,
∵AF=AF,
∴△GAF≌△EAF,
∴EF=GF,
∴GF=DF+DG=DF+BE,
即:EF=DF+BE.
(2)EF=DF-BE.
在DC上截取DH=BE,连接AH,如图②,

∵AD=AB,∠ADH=∠ABE=90°,
∴△ADH≌△ABE(SAS),
∴AH=AE,∠DAH=∠EAB,
∵∠EAF=∠EAB+∠BAF=45°,
∴∠DAH+∠BAF=45°,
∴∠HAF=45°=∠EAF,
∵AF=AF,
∴△HAF≌EAF(SAS),
∴HF=EF,
∵DF=DH+HF,
∴EF=DF-BE.
(3)如图③,

由(1)中结论可知:EF=DF+BE,
∵AB=BC=CD=AD=6,
设BE=x,则CE=6-x,
∵EF=5,
∴DF=5-x,
∴FC=1+x,
在Rt△CEF中,EF2=FC2+CE2,
∴25=(1+x)2+(6-x)2,
解得:x=2或x=3,
即BE的长为2或3.
看了如图,把一块含45°直角三角板...的网友还看了以下:
如图,三角形ABC中,分别从ABAC为边向ABC外作正三角形正四边形正五边形,BECD交于点O1) 2020-04-27 …
数学达人请进,一个三角形一个正方行一个圈代表三个数并且两个三角形相加等于三个正方形相加三个正方形等 2020-05-13 …
三角5个,正方6个,圆8个,三角的个数是全部的几分之几,正方的个数是三角和正方的几分之几?三角的个 2020-05-14 …
谁教我?求出圆形、三角形、正方形所代表的数圆形+三角形+正方形+正方形=10,三角形+正方形+三角 2020-06-06 …
有5个三角形,6个正方形,8个圆形!三角形的个数是全部的几分之几,正方形的个数是三角形+正方形,几 2020-06-09 …
将3个三角形,3个圆形,3个正方形放入方格中,史每一横形,每一竖形都有一个三角形,正方形,圆形,你 2020-06-19 …
正方形+正方形+三角形=8.3正方形-三角形=0.25正方形=()三角形=()正方形乘三角形=() 2020-06-27 …
正方型+凌形—倒三角=6倒三角—正三角+正方型=3凌形×正方型×倒三角=140凌形+倒三角+正方形 2020-07-14 …
如果正方形+圆+三角形+正方形=53圆+三角形+正方形+圆=46三角形+正方形+圆+三角形=49. 2020-07-17 …
1,一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中的三个是正三角形,正四边形,正 2020-12-25 …