早教吧作业答案频道 -->物理-->
如图所示,用一根长为L=1.0m不可伸长的细绳,一端固定在天花板上的O点,另一端系一小球A,在O点的正下方钉一钉子B,质量为m=lKg的小球由水平位置静止释放,取g=l0m/s2.(1)在O点的正下
题目详情
如图所示,用一根长为L=1.0m不可伸长的细绳,一端固定在天花板上的O点,另一端系一小球A,在O点的正下方钉一钉子B,质量为m=lKg的小球由水平位置静止释放,取g=l0m/s2.
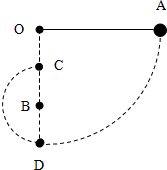
(1)在O点的正下方如果没有钉子B,小球摆到最低点D时,小球速度多大?(6分)细绳的拉力是多大?
(2)如果细绳的最大承受力为135N,要使细绳碰到B后小球能以B为圆心做完整的圆周运动,求钉子B离O点的可能距离.

(1)在O点的正下方如果没有钉子B,小球摆到最低点D时,小球速度多大?(6分)细绳的拉力是多大?
(2)如果细绳的最大承受力为135N,要使细绳碰到B后小球能以B为圆心做完整的圆周运动,求钉子B离O点的可能距离.
▼优质解答
答案和解析
(1)从A至D,应用动能定理,得:
mgL=
m
-0
变形得:vD=
=
=2
m/s
由圆周运动的规律及牛顿第二定律,有:
T-mg=m
代入数据,运算得:T=30N
(2)①当T为135N时,点B离O最远,设为S1,在最低点,由牛顿第二定律有:
T-mg=m
代入数值计算得:S1=0.84m
②设点B离O是最近的距离为S2,此时小球刚好能过最高点C.
在C点有,由牛顿第二定律有:mg=m
从D到C,应用动能定理有:
-mg•2(L-S2)=
m
-
m
由以上两式得:S2=0.6m
因此,B离O点的距离可能为0.6m至0.84m.
答:(1)小球摆到最低点D时,小球速度是2
m/s,细绳的拉力是30N.
(2)B离O点的距离可能为0.6m至0.84m.
mgL=
| 1 |
| 2 |
| v | 2 D |
变形得:vD=
| 2gL |
| 2×10×1 |
| 5 |
由圆周运动的规律及牛顿第二定律,有:
T-mg=m
| ||
| L |
代入数据,运算得:T=30N
(2)①当T为135N时,点B离O最远,设为S1,在最低点,由牛顿第二定律有:
T-mg=m
| ||
| L-S1 |
代入数值计算得:S1=0.84m
②设点B离O是最近的距离为S2,此时小球刚好能过最高点C.
在C点有,由牛顿第二定律有:mg=m
| ||
| L-S2 |
从D到C,应用动能定理有:
-mg•2(L-S2)=
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 D |
由以上两式得:S2=0.6m
因此,B离O点的距离可能为0.6m至0.84m.
答:(1)小球摆到最低点D时,小球速度是2
| 5 |
(2)B离O点的距离可能为0.6m至0.84m.
看了如图所示,用一根长为L=1.0...的网友还看了以下:
菊花为题的诗或词 2020-04-27 …
在古代怎样形容一个地方很美,与世无争,以桃花为主的段子,越长越好清静优雅 2020-05-13 …
△Ep这些量的值衡为正的吗?变化量和增量定义是什么?△Ek △Ep属于哪一种?△Ek △Ep有没有 2020-05-17 …
华北平原适宜发展()A、以水稻为主的水田农业B、以甜菜、棉花为主的绿洲农业C、以小麦、棉花为主的旱 2020-05-17 …
扔2个硬币,2个同为正的概率,1正1负的概率,正负各50%的概率,第1个为1/4,第2个为何是1/ 2020-06-02 …
一朵小花文章以一朵小花为题的作用 2020-06-05 …
以“孤芳自赏的花”为题的作文如题,写一篇,童话或寓言故事,字数为200~300字之间,注意语句优美 2020-06-12 …
扔两枚硬币,确定其中一枚为正,另一枚也为正的概率是多少?老师说:确定其中一枚为正,那么就有正正,正 2020-06-16 …
做简谐振动的小球速度最大值为3cm/s.振幅A=2cm.若从速度为正的最大值的某点开始计算时间,求 2020-06-17 …
某弹簧振子沿x轴的简谐振动图象如图所示,下列描述正确的是()A.t=1s时,振子的速度为零,加速度 2020-07-04 …