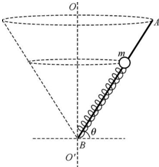
如图所示，光滑直杆AB长为L，B端固定一根劲度系数为k、原长为l0的轻弹簧，质量为m的小球套在光滑直杆上并与弹簧的上端连接．OO'为过B点的竖直轴，杆与水平面间的夹角始终为θ．（1

Question

如图所示，光滑直杆AB长为L，B端固定一根劲度系数为k、原长为l₀的轻弹簧，质量为m的小球套在光滑直杆上并与弹簧的上端连接．OO'为过B点的竖直轴，杆与水平面间的夹角始终为θ．

（1）杆保持静止状态，让小球从弹簧的原长位置静止释放，求小球释放瞬间的加速度大小a及小球速度最大时弹簧的压缩量△l₁；
（2）当小球随光滑直杆一起绕OO'轴匀速转动时，弹簧伸长量为△l₂，求匀速转动的角速度ω；
（3）若θ=30°，移去弹簧，当杆绕OO'轴以角速度ω₀=√((g)/(L))匀速转动时，小球恰好在杆上某一位置随杆在水平面内匀速转动，求小球离B点的距离L₀．

Answer 1

（1）小球从弹簧的原长位置静止释放时，根据牛顿第二定律有：
mgsin θ=ma
解得：a=gsin θ
小球速度最大时其加速度为零，则有：
k△l₁=mgsin θ
解得：△l₁=(mgsinθ)/(k)
（2）设弹簧伸长△l₂时，球受力如图所示，水平方向上有：
F_Nsin θ+k△l₂cos θ=mω²（l₀+△l₂）cos θ
竖直方向上有：F_Ncos θ-k△l₂sin θ-mg=0
解得：ω=√((k△l2-mgsinθ)/(mrcosθ))
（3）当杆绕OO'轴以角速度ω₀匀速转动时，设小球距离B点L₀，
此时有：mgtan θ=mL₀cos θ
解得：L₀=(gtanθ)/(cosθ)=(2)/(3)L
答：（1）杆保持静止状态，让小球从弹簧的原长位置静止释放，小球释放瞬间的加速度大小a及小球速度最大时弹簧的压缩量△l₁为(mgsinθ)/(k)；
（2）当小球随光滑直杆一起绕OO'轴匀速转动时，弹簧伸长量为△l₂，匀速转动的角速度ω为√((k△l2-mgsinθ)/(mrcosθ))；
（3）小球离B点的距离L₀为(2)/(3)L．