早教吧作业答案频道 -->数学-->
已知O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请说明理由
题目详情
已知O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.
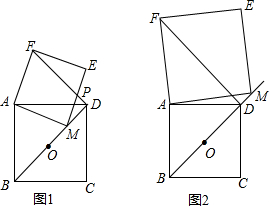
(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请说明理由;
(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由.
(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请说明理由;
(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由.

▼优质解答
答案和解析
(1)BM=DF,BM⊥DF.
理由:∵四边形ABCD、AMEF是正方形,
∴AF=AM,AD=AB,∠FAM=∠DAB=90°,
∴∠FAM-∠DAM=∠DAB-∠DAM,
即∠FAD=∠MAB,
∵在△FAD和△MAB中,
,
∴△FAD≌△MAB,
∴BM=DF,∠FDA=∠ABD=45°,
∵∠ADB=45°,
∴∠FDB=45°+45°=90°,
∴BM⊥DF,
即BM=DF,BM⊥DF.
(2)BM=DF,BM⊥DF都成立,
理由是:∵四边形ABCD和AMEF均为正方形,
∴AB=AD,AM=AF,∠BAD=∠MAF=90°,
∴∠FAM+∠DAM=∠DAB+∠DAM,
即∠FAD=∠MAB,
∵在△FAD和△MAB中,
,
∴△FAD≌△MAB,
∴BM=DF,∠ABM=∠ADF,
由正方形ABCD知,∠ABM=∠ADB=45°,
∴∠BDF=∠ADB+∠ADF=90°,
即BM⊥DF,
∴(1)中的结论仍成立.
理由:∵四边形ABCD、AMEF是正方形,
∴AF=AM,AD=AB,∠FAM=∠DAB=90°,
∴∠FAM-∠DAM=∠DAB-∠DAM,
即∠FAD=∠MAB,
∵在△FAD和△MAB中,
|
∴△FAD≌△MAB,
∴BM=DF,∠FDA=∠ABD=45°,
∵∠ADB=45°,
∴∠FDB=45°+45°=90°,
∴BM⊥DF,
即BM=DF,BM⊥DF.
(2)BM=DF,BM⊥DF都成立,
理由是:∵四边形ABCD和AMEF均为正方形,
∴AB=AD,AM=AF,∠BAD=∠MAF=90°,
∴∠FAM+∠DAM=∠DAB+∠DAM,
即∠FAD=∠MAB,
∵在△FAD和△MAB中,
|
∴△FAD≌△MAB,
∴BM=DF,∠ABM=∠ADF,
由正方形ABCD知,∠ABM=∠ADB=45°,
∴∠BDF=∠ADB+∠ADF=90°,
即BM⊥DF,
∴(1)中的结论仍成立.
看了已知O为正方形ABCD的中心,...的网友还看了以下:
关于信息技术()说法是正确的A当今时代,信息技术正以超越人们想象的速度发展B计算机技术就是通信技术 2020-04-25 …
关于发起理算任务,以下说法是正确的:( )A.当前报案下还存在未提交的立案任务,不能产生理算任务 2020-05-22 …
下面是有关Windows98的文件管理功能的一些叙述,其中哪个是正确的?A.当硬盘被分为多个分区时, 2020-05-23 …
在数据仓库中,下画哪一种说法是关于分析型数据的?A.当前的、准确的B.重复的、简单事务C.面向主题D 2020-05-23 …
下列关于关系模式的码的叙述中,哪一条是不正确的?A.当候选码多于一个时,选定其中一个作为主码B. 2020-05-23 …
下列关于关系模式的码的叙述中,哪一项是不正确的?A.当候选码多于一个时,选定其中一个作为主码B. 2020-05-24 …
关于出生后血液循环的变化以下哪项是不正确的A.当左心房压力超过右心房时卵圆孔发生功能上关闭B. 2020-06-06 …
关于血尿的临床特点,下列哪项是错误的()A.当尿液为碱性时,颜色呈红色B.当尿液为酸性时,颜色呈棕 2020-06-07 …
依次填入下列横线上的关联词语,最恰当的一组是()①国外有种说法,“人的一生中只有两件事是逃不过去的 2020-06-19 …
机械工程关于孔的最大实体原则如Φ5(+0.1/0)对称度0.1最大实体原则那么以下哪种是对的?A当 2020-07-30 …